4. Fuerzas centrales

Pertenece al temario de Fisica

Suponemos que un planeta que gira alrededor del sol soporta una fuerza gravitatoria dirigida hacia el sol y que depende sólo de r. Esta fuerza gravitatoria es una fuerza central y es conservativa.

[math]\displaystyle{ \vec F_g = \frac {-GMm}{r^2} \hat u_r }[/math]

Otros ejemplos de fuerzas centrales son: la fuerza centrípeta, la fuerza recuperadora del m.a.s., la fuerza electrostática de coulomb…

Momento de torsión de una fuerza respecto a un punto

Cuando se ejerce una fuerza sobre un cuerpo rígido que pueda girar alrededor de un eje, dicho cuerpo realiza una rotación, siempre y cuando la fuerza no se dirija o provenga de dicho eje.

La capacidad de una fuerza de hacer girar un cuerpo alrededor de un eje se define como momento de torsión de una fuerza o momento de una fuerza (M).

@@@@@@Dibujo

Aplicamos una fuerza que forma un angulo [math]\displaystyle{ \theta }[/math] sobre el eje OY, descomponemos F en [math]\displaystyle{ \vec F_y }[/math] y [math]\displaystyle{ \vec F_z }[/math]. [math]\displaystyle{ \vec F_z }[/math] dista [math]\displaystyle{ \vec r }[/math] del origen. [math]\displaystyle{ \vec F_y }[/math] esta sobre el eje y, es decir, tiene una distancia nula al origen, por lo tanto, solo [math]\displaystyle{ \vec F_z }[/math] tiene capacidad para el giro, y [math]\displaystyle{ \vec F_y }[/math] tendrá [math]\displaystyle{ M=0 }[/math]

• Momento Fz:

[math]\displaystyle{ M=F r sin \theta = F d = F_{z} r }[/math]

d: es el brazo del momento o palanca y representa la distancia desde el centro de rotación hasta la línea de acción de fuerzas. [math]\displaystyle{ d=r sin \theta }[/math]

• Momento Fy:

[math]\displaystyle{ M=F_y r sin \theta }[/math]

Por definicion: [math]\displaystyle{ \vec M = \vec r x \vec F }[/math] donde r es el vector posicion respecto del origen del punto de aplicacion de la fuerza

@##@~dibujo¶ [math]\displaystyle{ \vec M \perp \vec F }[/math] [math]\displaystyle{ \vec M \perp \vec r }[/math]

El sentido del momento depende de camino mas corto entre los dos vectores, siendo el antihorario positivo y el horario negativo.

El resultado de un producto vectorial es un vector perpendicular a r y a F. Por tanto, M es perpendicular a r y F.

Para saber el sentido de M tambien podemos usar la regla del sacacorchos.

Momento de torsión de una fuerza central

Todas las fuerzas centrales tienen el momento de torsión nulo.

Momento angular de una partícula

Momento lineal o cantidad de movimiento de una partícula:

Conclusiones: -el valor de la dirección de L depende del punto donde se toma el momento.

-el momento angular máximo se obtiene si y solo si el senβ=1 y eso será cuadno el ángulo sea 90º

a) momento angular de un sistema de partículas

El momento angular de un sistema de partículas se obtiene sumando los momentos angulares de cada una de las partículas.

Momento de inercia, I: mide la inercia o resistencia que ofrece el sólido para cambiar su velocidad de giro cuando sobre él se aplica un momento de torsión de una fuerza:

b) momento angular terrestre

Distinguimos dos tipos de movimiento de la Tierra y por lo tanto dos tipos de momento angulares.

• Momento orbital: es el momento que se crea debido al movimiento de la tierra alrededor del sol.

Suponemos que la Tierra se encuentra en el punto A: θ=90º

• Momento angular intrínseco: es el momento que se crea debido a la rotación de la Tierra sobre su eje. Sabemos que la Tierra es una esfera homogénea y maciza, y por tanto el omento de inercia I:

c) relación entre el momento de torsión y el momento angular:

-momento de torsión de una Fuerza:

-momento angular de una partícula:

Para estudiar la relación entre ambos momentos derivamos el momento angular (L) respecto del tiempo:

El momento de una fuerza sobre una partícula en un punto P es igual a la variación que experimenta el momento angular de la partícula

• Conservación del momento angular : hemos deducido que M= dL/dt y además sabemos que el momento de torsión de una fuerza central es nula. Deducimos entonces que el momento angular de las fuerzas centrales será constante.

• Ecuación fundamental de la dinámica de rotación. Si aplicamos el momento angular a un sólido rígido L=Iw

Momento angular y movimiento planetario. 2ª Ley de Kepler

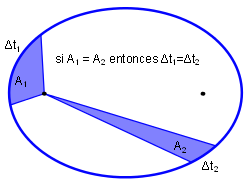
La ley de las áreas dice: las áreas barridas por el radio vector que une el sol con un planeta son directamente proporcionales al tiempo en barrerlas.

Los planetas y los satélites se mueven bajo fuerzas centrales. Éstos tendrán el momento angula constante

-Constante la dirección de L

-Constante el sentido de L

-Constante en módulo |L|

• Si L es constante en dirección implica que el movimiento de la partícula ocurre en un plano

• Si L es constante en sentido indica que la partícula recorre siempre la trayectoria en el mismo sentido.
• Si L es constante en módulo cumplirá la 2ª Ley de Kepler:

La ley de las áreas: toda partícula que se mueva bajo una fuerza central lo hace con una velocidad areolar constante

Suponemos órbitas elípticas alrededor del sol

Un planeta que gira alrededor del sol va más deprisa en el perihelio que cuando se encuentra en el afelio.

En el ejemplo dibujado, el planeta tarda lo mismo en ir del punto P1 a P2 que de P3 a P4, por lo tanto, siguiedo la ley de las áreas, el A1=A2