Diferencia entre revisiones de «Memoria de practicas: Circuito RC en Alterna»
| Línea 62: | Línea 62: | ||
<math>Z_T=Z_R+Z_C= 3300_{0^\circ}+3183.09_{-90^\circ} = \sqrt{3300^2+3183.09^2}_{tan^{-1} \frac{-3183.09}{3300}} = 4584.98_{-43.96^\circ}\Omega</math> | <math>Z_T=Z_R+Z_C= 3300_{0^\circ}+3183.09_{-90^\circ} = \sqrt{3300^2+3183.09^2}_{tan^{-1} \frac{-3183.09}{3300}} = 4584.98_{-43.96^\circ}\Omega</math> | ||
<br> | <br> | ||
<math>V=i\cdotZ=|i||Z|_{\ | <math>V=i\cdotZ=|i||Z|_{\phi_i+\phi_Z</math> | ||
Revisión del 17:06 30 oct 2013
Introduccion y objetivos
Esta practica se divide en dos partes, una parte previa realizada mediante simulador y la parte practica con sus correspondientes calculos previos. Los objetivos de la simulacion son comprender el concepto de filtrado, la impedancia y el desfase que se produce en este proceso y entender el comportamiento del condensador. Por su parte, la parte practica tiene como objetivo aplicar los conocimientos de la simulacion en la realidad y perfeccionar el manejo de la instrumentacion.
Lista de materiales
- Polimetro Promax PD693
- Conversor BNC
- Generador de impulsos HP 33120A
- Osciloscopio Tektronix TDS210
- Tablero de laboratorio
- Condensador
- Resistencia
- Sonda Tektronix P6112
Simulacion
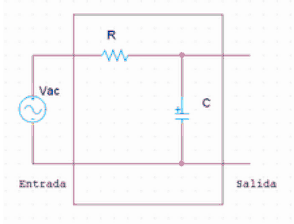
Simularemos en ORCAD el circuito que posteriormente montaremos. El condensador de este circuito tiene una capacidad de 1 µF y la resistencia vale 3,3 kΩ.
El uso de un condensador electrolitico en corriente alterna es adecuado dado que su salida tambien será corriente alterna. Si no utilizasemos un condensador electrolitico, el condensador se cargaria en el primer momento, y despues no dejará pasar corriente.
Compararemos la respuesta del filtro que forma este circuito a varios valores de tension y frecuencia. Comenzamos por una señal de 8V de amplitud (de pico) y 10Hz de frecuencia.
[[]]
El primer maximo que se representa es de la señal de salida, el segundo, de la señal de entrada. El desfase entre ambas señales es de 3.6ms.
Represenatamos ahora una señal de 8V de amplitud (de pico) y 50Hz de frecuencia.
El primer maximo que se representa es de la señal de entrada y el segundo, el de la señal de salida. EL desfase entre ambas señales es de 2.56ms
La siguente es una señal de 8V de amplitud (de pico) y 75Hz de frecuencia.
[[]]
El primer maximo que se representa es de la señal de entrada y el segundo, el de la señal de salida. EL desfase entre ambas señales es de 2.15ms.
La siguente es una señal de 8V de amplitud (de pico) y 150Hz de frecuencia.
[[]]
El primer maximo que se representa es de la señal de entrada y el segundo, el de la señal de salida. EL desfase entre ambas señales es de ms.
Por ultimo, representamos una señal de 1kHz de frecuencia y 8V de amplitud (de pico).
El primer maximo que se representa es de la señal de entrada y el segundo, el de la señal de salida. EL desfase entre ambas señales es de ms.
Ahora cambiamos el modo del simulador, de Time Domain, que estabamos usando hasta ahora, a AC Sweep/Noise. Asimismo, tambien cambiamos la fuente por una fuente VDC. Esto nos va a permitir hacer un barrido por todas las frecuencias y determinar en cuales se produce el filtrado.
Cálculos previos
En este caso la fuente da 10V de tension de pico a una frecuencia de 50Hz, la resistencia es de [math]\displaystyle{ 3.3k\Omega }[/math] y el condensador vale [math]\displaystyle{ 1\mu F }[/math]
La impedancia total del circuito viene dada por la impedancia de la resistencia y la del condensador.
[math]\displaystyle{ Z_T=Z_R+Z_C }[/math]
[math]\displaystyle{ Z_R=3.3k\Omega \ _{0^\circ} }[/math]
[math]\displaystyle{ Z_C=\frac {1}{2\pi f C}_{-90^\circ}=\frac {1}{2\pi\cdot 50 \cdot 1\cdot10^{-6}}_{-90^\circ}=3183,09\Omega \ _{-90^\circ} }[/math]
[math]\displaystyle{ Z_T=Z_R+Z_C= 3300_{0^\circ}+3183.09_{-90^\circ} = \sqrt{3300^2+3183.09^2}_{tan^{-1} \frac{-3183.09}{3300}} = 4584.98_{-43.96^\circ}\Omega }[/math]
[math]\displaystyle{ V=i\cdotZ=|i||Z|_{\phi_i+\phi_Z }[/math]