Diferencia entre revisiones de «Memoria de practicas: Circuito RC en Alterna»
| (No se muestran 27 ediciones intermedias del mismo usuario) | |||
| Línea 51: | Línea 51: | ||
Ahora cambiamos el modo del simulador, de Time Domain, que estábamos usando hasta ahora, a AC Sweep/Noise. Asimismo, también cambiamos la fuente por una fuente VDC. Esto nos va a permitir hacer un barrido por todas las frecuencias y determinar en cuales se produce el filtrado. | Ahora cambiamos el modo del simulador, de Time Domain, que estábamos usando hasta ahora, a AC Sweep/Noise. Asimismo, también cambiamos la fuente por una fuente VDC. Esto nos va a permitir hacer un barrido por todas las frecuencias y determinar en cuales se produce el filtrado. | ||
Tenemos dos formas de ver el barrido en frecuencia. Una es en lineal: | |||
[[Archivo:Sweeplineal.PNG]] | |||
La otra es en logaritmico. | |||
[[Archivo:Sweeplog.PNG]] | |||
Se define la frecuencia de corte de un filtro a aquella para que la potencia de la señal de salida cae a la mitad con respecto a la de entrada. | |||
<math>P=V \cdot I= \frac{V^2}{R} \Rightarrow \frac{P_{salida}}{P_{entrada}} = \frac{V^2_{salida}/R}{V^2_{entrada}/R}= (\frac{V_{salida}}{V_{entrada}})^2 = \frac {1}{2} \Rightarrow \frac{V_{salida}}{V_{entrada}} = \frac {1}{2}</math> | |||
Por tanto, decir que la potencia cae a la mitad es lo mismo que decir que la tensión es √2 veces menor. La frecuencia de corte en esta gráfica es de 48Hz. | |||
Asimismo, si utilizamos la formula <math>f_{corte}= \frac {1}{2\pi RC}</math> la frecuencia de corte nos da 48,22Hz. | |||
Para hacer un filtro con una frecuencia de corte mas alta, por ejemplo 250Hz, podemos disminuir la resistencia o el condensador. | |||
Si se invierten la resistencia y el condensador se produce el efecto contrario, creando un filtro paso alto. | |||
Un filtro es tanto mejor cuanto más selectivo es. Un filtro es muy selectivo cuando la transición entre la banda de paso (banda de frecuencias que deja pasar) y las frecuencias más allá de la frecuencia de corte es muy abrupta. Este filtro no es nada selectivo, dado que la pendiente es muy poco abrupta. | |||
== Cálculos y cuestiones previas == | == Cálculos y cuestiones previas == | ||
[[Archivo:circuitorcalterna.png|center| | [[Archivo:circuitorcalterna.png|center|175px]] | ||
En este caso la fuente da 10V de tensión de pico a una frecuencia de 50Hz, la resistencia es de <math>3.3k\Omega</math> y el condensador vale <math>1\mu F</math> | En este caso la fuente da 10V de tensión de pico a una frecuencia de 50Hz, la resistencia es de <math>3.3k\Omega</math> y el condensador vale <math>1\mu F</math> | ||
'''En primer lugar, calcula y dibuja una gráfica con la corriente y la tensión del circuito si no colocáramos el condensador. ¿Estarán desfasadas?''' | |||
<math>V=IR\Rightarrow I=\frac {V}{R}=\frac {10}{3300}=0.003A</math> | |||
[[Archivo:Preguntasincondensador.png|300px]] | |||
A pesar de que en la imagen no se aprecia, no estarán desfasadas, dado que la resistencia no aplica desfase alguno a la corriente. | |||
'''Después, ya con el condensador, calcula la impedancia total del circuito y vuelve a dibujar la gráfica con la tensión y la corriente. ¿Circula más o menos corriente que antes? ¿Están desfasadas? ¿Por qué? Piensa cómo puedes ver ese desfase en el osciloscopio.''' | |||
La impedancia total del circuito viene dada por la impedancia de la resistencia y la del condensador. | |||
<br> | |||
<math>V_C=i\cdot Z_C = |i||Z_C|_{\phi_i+\phi_Z_c}= 2.18\cdot 10^{-3}\cdot 3183.09_{44+(-90)^\circ}= 6.94_{-46^\circ}</math> | <math>Z_T=Z_R+Z_C</math><br><math>Z_R=3.3k\Omega \ _{0^\circ}</math><br><math>Z_C=\frac {1}{2\pi f C}_{-90^\circ}=\frac {1}{2\pi\cdot 50 \cdot 1\cdot10^{-6}}_{-90^\circ}=3183,09\Omega \ _{-90^\circ}</math><br><math>Z_T=Z_R+Z_C= 3300_{0^\circ}+3183.09_{-90^\circ} = \sqrt{3300^2+3183.09^2}_{tan^{-1} \frac{-3183.09}{3300}} = 4584.98_{-43.96^\circ}\Omega</math> | ||
Nótese que la resistencia y el condensador están en serie, por lo que su intensidad será igual y tendrán diferente tensión. | |||
<math>V=i\cdot Z \Rightarrow i=\frac{V}{Z}=\frac {|V|}{|Z|}_{\phi_V-\phi_Z}=\frac {|10|}{|4584.98|}_{0-(-44)^\circ} = 2.18\cdot 10^{-3}\ _{44^\circ}</math> | |||
Circula menos corriente que antes, dado que el condensador también ofrece cierta resistencia. Están desfasadas, dado que la intensidad resulta de los ciclos de carga y descarga del condensador. | |||
'''Calcula la tensión en la resistencia VR y la tensión en el condensador VC. Dibújalas junto con la tensión del generador, en forma de gráfico temporal y con vectores.''' | |||
<math>V_R=i\cdot Z_R = |i||Z_R|_{\phi_i+\phi_Z_R}= 2.18\cdot 10^{-3}\cdot 3300_{44+0^\circ}= 7.197_{44^\circ}</math><br><math>V_C=i\cdot Z_C = |i||Z_C|_{\phi_i+\phi_Z_c}= 2.18\cdot 10^{-3}\cdot 3183.09_{44+(-90)^\circ}= 6.94_{-46^\circ}</math> | |||
[[Archivo:Tensionesvarias.png|300px]] | |||
'''Si en vez de un generador de alterna hubiéramos puesto la fuente de alimentación de continua, ¿qué hubiera sucedido? ¿Cómo se comporta el condensador y la bobina en continua? ¿Y en frecuencias muy bajas? ¿Y en frecuencias muy altas? Razona''' | |||
El condensador en corriente continua se carga y, al no haber mas variación de corriente, tampoco varia su carga, por lo que actúa como un circuito abierto. La bobina, sin embargo, actúa como un cable, por esa misma falta de variación. La bobina genera alrededor de si un campo magnético, que varia al variar la corriente, generando tensión. El condensador actúa de manera contraria, respondiendo con corriente a las variaciones de tensión. | |||
En frecuencias muy bajas se comportaran como en corriente continua. En frecuencias muy altas, los condensadores actúan como simples conductores, dado que cuanta mas alta es la frecuencia mas baja es la impedancia; mientras que las bobinas tienen cada vez mas impedancia al aumentar la frecuencia, por lo que tienden a ser un circuito abierto. | |||
'''¿Cómo tienes que usar el polímetro para medir en alterna? ¿qué valor estarías midiendo? ¿Puedes medir corrientes con el osciloscopio? ¿Y con el polímetro?''' | |||
Si quieres medir tensión de corriente alterna con el polimetro, debes ponerlo en posición de tensión alterna. Así medirás la tensión efectiva. La intensidad no se puede medir con el osciloscopio, si con el polímetro en posición de corriente alterna. | |||
'''Imagina que esa RC son los componentes internos de un circuito que tú no conoces y del que sólo ves su entrada (Vac) y su salida (VC) ¿Qué desfase y qué diferencia de amplitud hay entre la Vac (entrada) y la VC (salida)? Calcula esas diferencias si la frecuencia de la señal de entrada fuera de 50, 75, 150 y 1kHz y representa la gráfica Vac/ VC ¿Cómo dirías que se está comportando el circuito?¿Podrías explicar qué es un filtro? ¿Qué tipos de filtros hay y cómo funcionan? Incluye los símbolos con los que se representan.''' | |||
[[Archivo:Vac-vc.png|260px|right]] | |||
Tomando como referencia los datos de la simulación, el factor entre la entrada y la salida es de 0.97 en 10Hz, 0.69 en 50Hz, 0.63 en 75Hz, 0.42 en 150Hz y 0.08 en 1kHz. | |||
Un filtro es un conjunto de elementos electrónicos que ejerce oposición a unas frecuencias concretas, ya sean todas las frecuencias hasta una concreta, a partir de una concreta, una banda alrededor de una frecuencia o todas las frecuencias menos una banda. | |||
En este caso tenemos un filtro paso bajo, que deja pasar las frecuencias hasta una concreta y a partir de esa ejerce oposición a todas. | |||
Los símbolos que lo representan son los siguientes: | |||
[[Archivo:Filtros-simbolos.gif]] | |||
'''Imagina que en lugar de un circuito tan sencillo de R y C, una señal compuesta de distintas frecuencias atraviesa un circuito más complejo con R, C y L, en serie/paralelo etc. ¿Qué les sucederá a las diferentes frecuencias en su “carrera” a través del circuito? ¿Qué consecuencias tiene esto en la señal de salida?''' | |||
Dependiendo de la colocación de los elemento, las distintas frecuencias se irán desfasando y disminuirán su amplitud. La señal de salida se verá mermada, desfasada y filtrada. | |||
== Medidas== | |||
'''Comprueba todos los cálculos que has hecho, realizando las medidas de valores de pico, eficaces (tanto con el osciloscopio como con el polímetro), y desfases.''' | |||
{| class="wikitable" | |||
! V | |||
! R | |||
! C | |||
! T | |||
|- | |||
! P | |||
| 7.4V | |||
| 6.8V | |||
| 9.8V | |||
|- | |||
! PP | |||
| 14.8V | |||
| 13V | |||
| 19V | |||
|- | |||
! RMS | |||
| 5.1V | |||
| 4.12V | |||
| 6.78V | |||
|} | |||
La intensidad total es de 0.00203A, el desfase entre la tensión del condensador y la del generador es de 2.6ms y el desfase entre la tensión de la resistencia y la del generador es de 2.4ms. | |||
En este apartado se obvia mencionar explicitamente las mediciones con el polimetro dado que apenas se diferencian con las medidas del osciloscopio. | |||
'''Comprueba la tensión de salida, comparándola con la entrada (una en cada canal del osciloscopio) para todas las frecuencias indicadas.''' | |||
{| class="wikitable" | |||
! | |||
! 50Hz | |||
! 75Hz | |||
! 150Hz | |||
! 1kHz | |||
|- | |||
! <math>V_T (PP)</math> | |||
| 20.8V | |||
| 20.6V | |||
| 20.5V | |||
| 20.7V | |||
|- | |||
! <math>V_C (PP)</math> | |||
| 14.4V | |||
| 11.4V | |||
| 6.6V | |||
| 1.2V | |||
|- | |||
! <math>\phi</math> | |||
| 2.6ms | |||
| 2.2ms | |||
| 1.4ms | |||
| <math>240\mu s</math> | |||
|} | |||
'''Compara la señal de salida cuando la entrada es una onda cuadrada. Pregunta al profesor para que te enseñe a ver el espectro en frecuencia de las señales. ¿Cuál es el espectro a la entrada? ¿Cómo es a la salida? ¿Cómo está actuando el filtro? Comenta tus conclusiones.''' | |||
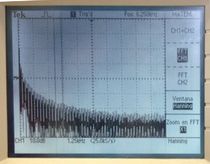
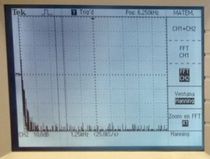
[[Archivo:Comparacion-cuadrada.jpg|210px]][[Archivo:Espectro-entrada-cuadrada.jpg|210px]][[Archivo:Espectro-salida-cuadrada.jpg|210px]] | |||
En este caso el filtro es un paso bajo, por lo que elimina los cambios mas bruscos. La onda cuadrada contiene cambios muy bruscos, por lo que al suavizarlos, la transforma en lo que vemos en la primera imagen. Respecto a las dos restantes, vemos como actúa el filtro en frecuencia, conservando la energía en las frecuencias bajas y reduciéndola en las frecuencias altas. | |||
'''¿Cómo colocarías R y C para hacer un filtro paso alto?''' | |||
En posiciones inversas a las de este esquema, en primer lugar el condensador y después la resistencia. | |||
Revisión actual del 10:59 31 oct 2013
Introducción y objetivos
Esta practica se divide en dos partes, una parte previa realizada mediante simulador y la parte practica con sus correspondientes cálculos previos. Los objetivos de la simulación son comprender el concepto de filtrado, la impedancia y el desfase que se produce en este proceso y entender el comportamiento del condensador. Por su parte, la parte practica tiene como objetivo aplicar los conocimientos de la simulación en la realidad y perfeccionar el manejo de la instrumentación.
Lista de materiales
- Polimetro Promax PD693
- Conversor BNC
- Generador de impulsos HP 33120A
- Osciloscopio Tektronix TDS210
- Tablero de laboratorio
- Condensador
- Resistencia
- Sonda Tektronix P6112
Simulación
Simularemos en ORCAD el circuito que posteriormente montaremos. El condensador de este circuito tiene una capacidad de 1 µF y la resistencia vale 3,3 kΩ.
El uso de un condensador electrolítico en corriente alterna es adecuado dado que su salida también será corriente alterna. Si no utilizásemos un condensador electrolítico, el condensador se cargaría en el primer momento, y después no dejará pasar corriente.
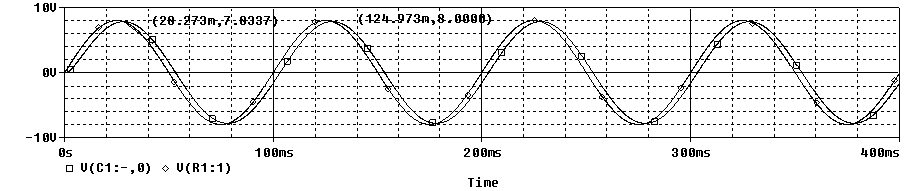
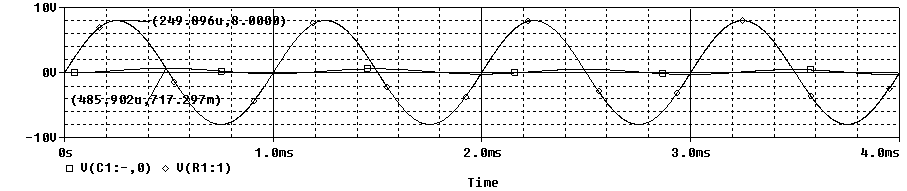
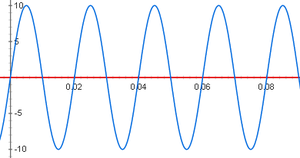
Compararemos la respuesta del filtro que forma este circuito a varios valores de tensión y frecuencia. Comenzamos por una señal de 8V de amplitud (de pico) y 10Hz de frecuencia.
El primer máximo que se representa es de la señal de salida, el segundo, de la señal de entrada. El desfase entre ambas señales es de 3.6ms.
Representamos ahora una señal de 8V de amplitud (de pico) y 50Hz de frecuencia.
El primer máximo que se representa es de la señal de entrada y el segundo, el de la señal de salida. El desfase entre ambas señales es de 2.56ms
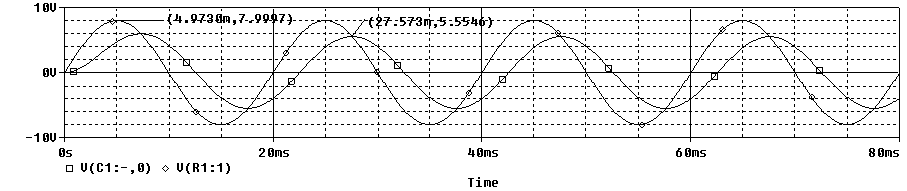
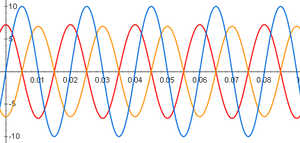
La siguente es una señal de 8V de amplitud (de pico) y 75Hz de frecuencia.
El primer máximo que se representa es de la señal de entrada y el segundo, el de la señal de salida. El desfase entre ambas señales es de 2.15ms.
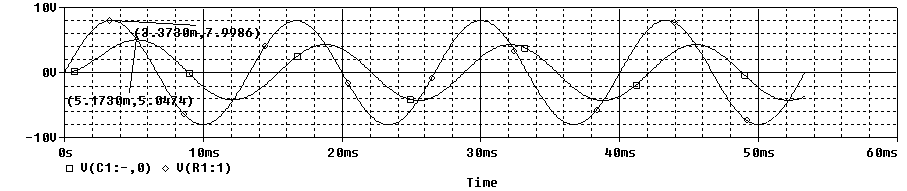
La siguente es una señal de 8V de amplitud (de pico) y 150Hz de frecuencia.
El primer máximo que se representa es de la señal de entrada y el segundo, el de la señal de salida. El desfase entre ambas señales es de 1.51ms.
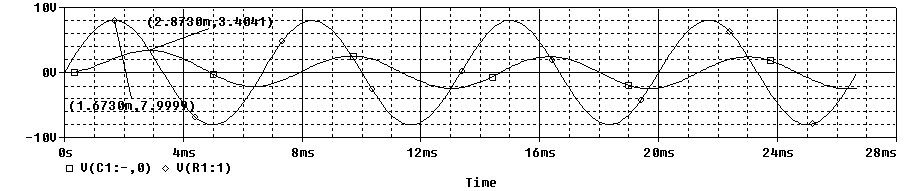
Por ultimo, representamos una señal de 1kHz de frecuencia y 8V de amplitud (de pico).
El primer máximo que se representa es de la señal de entrada y el segundo, el de la señal de salida. El desfase entre ambas señales es de 0.24ms.
Ahora cambiamos el modo del simulador, de Time Domain, que estábamos usando hasta ahora, a AC Sweep/Noise. Asimismo, también cambiamos la fuente por una fuente VDC. Esto nos va a permitir hacer un barrido por todas las frecuencias y determinar en cuales se produce el filtrado.
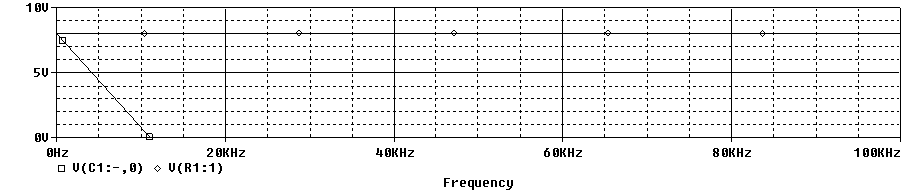
Tenemos dos formas de ver el barrido en frecuencia. Una es en lineal:
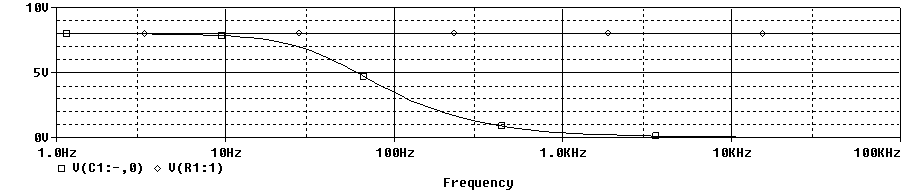
La otra es en logaritmico.
Se define la frecuencia de corte de un filtro a aquella para que la potencia de la señal de salida cae a la mitad con respecto a la de entrada.
[math]\displaystyle{ P=V \cdot I= \frac{V^2}{R} \Rightarrow \frac{P_{salida}}{P_{entrada}} = \frac{V^2_{salida}/R}{V^2_{entrada}/R}= (\frac{V_{salida}}{V_{entrada}})^2 = \frac {1}{2} \Rightarrow \frac{V_{salida}}{V_{entrada}} = \frac {1}{2} }[/math]
Por tanto, decir que la potencia cae a la mitad es lo mismo que decir que la tensión es √2 veces menor. La frecuencia de corte en esta gráfica es de 48Hz.
Asimismo, si utilizamos la formula [math]\displaystyle{ f_{corte}= \frac {1}{2\pi RC} }[/math] la frecuencia de corte nos da 48,22Hz.
Para hacer un filtro con una frecuencia de corte mas alta, por ejemplo 250Hz, podemos disminuir la resistencia o el condensador.
Si se invierten la resistencia y el condensador se produce el efecto contrario, creando un filtro paso alto.
Un filtro es tanto mejor cuanto más selectivo es. Un filtro es muy selectivo cuando la transición entre la banda de paso (banda de frecuencias que deja pasar) y las frecuencias más allá de la frecuencia de corte es muy abrupta. Este filtro no es nada selectivo, dado que la pendiente es muy poco abrupta.
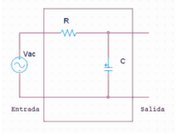
Cálculos y cuestiones previas
En este caso la fuente da 10V de tensión de pico a una frecuencia de 50Hz, la resistencia es de [math]\displaystyle{ 3.3k\Omega }[/math] y el condensador vale [math]\displaystyle{ 1\mu F }[/math]
En primer lugar, calcula y dibuja una gráfica con la corriente y la tensión del circuito si no colocáramos el condensador. ¿Estarán desfasadas?
[math]\displaystyle{ V=IR\Rightarrow I=\frac {V}{R}=\frac {10}{3300}=0.003A }[/math]
A pesar de que en la imagen no se aprecia, no estarán desfasadas, dado que la resistencia no aplica desfase alguno a la corriente.
Después, ya con el condensador, calcula la impedancia total del circuito y vuelve a dibujar la gráfica con la tensión y la corriente. ¿Circula más o menos corriente que antes? ¿Están desfasadas? ¿Por qué? Piensa cómo puedes ver ese desfase en el osciloscopio.
La impedancia total del circuito viene dada por la impedancia de la resistencia y la del condensador.
[math]\displaystyle{ Z_T=Z_R+Z_C }[/math]
[math]\displaystyle{ Z_R=3.3k\Omega \ _{0^\circ} }[/math]
[math]\displaystyle{ Z_C=\frac {1}{2\pi f C}_{-90^\circ}=\frac {1}{2\pi\cdot 50 \cdot 1\cdot10^{-6}}_{-90^\circ}=3183,09\Omega \ _{-90^\circ} }[/math]
[math]\displaystyle{ Z_T=Z_R+Z_C= 3300_{0^\circ}+3183.09_{-90^\circ} = \sqrt{3300^2+3183.09^2}_{tan^{-1} \frac{-3183.09}{3300}} = 4584.98_{-43.96^\circ}\Omega }[/math]
Nótese que la resistencia y el condensador están en serie, por lo que su intensidad será igual y tendrán diferente tensión.
[math]\displaystyle{ V=i\cdot Z \Rightarrow i=\frac{V}{Z}=\frac {|V|}{|Z|}_{\phi_V-\phi_Z}=\frac {|10|}{|4584.98|}_{0-(-44)^\circ} = 2.18\cdot 10^{-3}\ _{44^\circ} }[/math]
Circula menos corriente que antes, dado que el condensador también ofrece cierta resistencia. Están desfasadas, dado que la intensidad resulta de los ciclos de carga y descarga del condensador.
Calcula la tensión en la resistencia VR y la tensión en el condensador VC. Dibújalas junto con la tensión del generador, en forma de gráfico temporal y con vectores.
[math]\displaystyle{ V_R=i\cdot Z_R = |i||Z_R|_{\phi_i+\phi_Z_R}= 2.18\cdot 10^{-3}\cdot 3300_{44+0^\circ}= 7.197_{44^\circ} }[/math]
[math]\displaystyle{ V_C=i\cdot Z_C = |i||Z_C|_{\phi_i+\phi_Z_c}= 2.18\cdot 10^{-3}\cdot 3183.09_{44+(-90)^\circ}= 6.94_{-46^\circ} }[/math]
Si en vez de un generador de alterna hubiéramos puesto la fuente de alimentación de continua, ¿qué hubiera sucedido? ¿Cómo se comporta el condensador y la bobina en continua? ¿Y en frecuencias muy bajas? ¿Y en frecuencias muy altas? Razona
El condensador en corriente continua se carga y, al no haber mas variación de corriente, tampoco varia su carga, por lo que actúa como un circuito abierto. La bobina, sin embargo, actúa como un cable, por esa misma falta de variación. La bobina genera alrededor de si un campo magnético, que varia al variar la corriente, generando tensión. El condensador actúa de manera contraria, respondiendo con corriente a las variaciones de tensión.
En frecuencias muy bajas se comportaran como en corriente continua. En frecuencias muy altas, los condensadores actúan como simples conductores, dado que cuanta mas alta es la frecuencia mas baja es la impedancia; mientras que las bobinas tienen cada vez mas impedancia al aumentar la frecuencia, por lo que tienden a ser un circuito abierto.
¿Cómo tienes que usar el polímetro para medir en alterna? ¿qué valor estarías midiendo? ¿Puedes medir corrientes con el osciloscopio? ¿Y con el polímetro?
Si quieres medir tensión de corriente alterna con el polimetro, debes ponerlo en posición de tensión alterna. Así medirás la tensión efectiva. La intensidad no se puede medir con el osciloscopio, si con el polímetro en posición de corriente alterna.
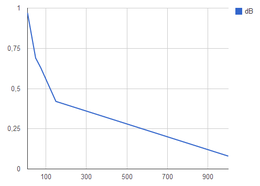
Imagina que esa RC son los componentes internos de un circuito que tú no conoces y del que sólo ves su entrada (Vac) y su salida (VC) ¿Qué desfase y qué diferencia de amplitud hay entre la Vac (entrada) y la VC (salida)? Calcula esas diferencias si la frecuencia de la señal de entrada fuera de 50, 75, 150 y 1kHz y representa la gráfica Vac/ VC ¿Cómo dirías que se está comportando el circuito?¿Podrías explicar qué es un filtro? ¿Qué tipos de filtros hay y cómo funcionan? Incluye los símbolos con los que se representan.
Tomando como referencia los datos de la simulación, el factor entre la entrada y la salida es de 0.97 en 10Hz, 0.69 en 50Hz, 0.63 en 75Hz, 0.42 en 150Hz y 0.08 en 1kHz.
Un filtro es un conjunto de elementos electrónicos que ejerce oposición a unas frecuencias concretas, ya sean todas las frecuencias hasta una concreta, a partir de una concreta, una banda alrededor de una frecuencia o todas las frecuencias menos una banda.
En este caso tenemos un filtro paso bajo, que deja pasar las frecuencias hasta una concreta y a partir de esa ejerce oposición a todas.
Los símbolos que lo representan son los siguientes:
Imagina que en lugar de un circuito tan sencillo de R y C, una señal compuesta de distintas frecuencias atraviesa un circuito más complejo con R, C y L, en serie/paralelo etc. ¿Qué les sucederá a las diferentes frecuencias en su “carrera” a través del circuito? ¿Qué consecuencias tiene esto en la señal de salida?
Dependiendo de la colocación de los elemento, las distintas frecuencias se irán desfasando y disminuirán su amplitud. La señal de salida se verá mermada, desfasada y filtrada.
Medidas
Comprueba todos los cálculos que has hecho, realizando las medidas de valores de pico, eficaces (tanto con el osciloscopio como con el polímetro), y desfases.
| V | R | C | T |
|---|---|---|---|
| P | 7.4V | 6.8V | 9.8V |
| PP | 14.8V | 13V | 19V |
| RMS | 5.1V | 4.12V | 6.78V |
La intensidad total es de 0.00203A, el desfase entre la tensión del condensador y la del generador es de 2.6ms y el desfase entre la tensión de la resistencia y la del generador es de 2.4ms.
En este apartado se obvia mencionar explicitamente las mediciones con el polimetro dado que apenas se diferencian con las medidas del osciloscopio.
Comprueba la tensión de salida, comparándola con la entrada (una en cada canal del osciloscopio) para todas las frecuencias indicadas.
| 50Hz | 75Hz | 150Hz | 1kHz | |
|---|---|---|---|---|
| [math]\displaystyle{ V_T (PP) }[/math] | 20.8V | 20.6V | 20.5V | 20.7V |
| [math]\displaystyle{ V_C (PP) }[/math] | 14.4V | 11.4V | 6.6V | 1.2V |
| [math]\displaystyle{ \phi }[/math] | 2.6ms | 2.2ms | 1.4ms | [math]\displaystyle{ 240\mu s }[/math] |
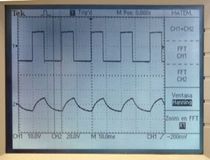
Compara la señal de salida cuando la entrada es una onda cuadrada. Pregunta al profesor para que te enseñe a ver el espectro en frecuencia de las señales. ¿Cuál es el espectro a la entrada? ¿Cómo es a la salida? ¿Cómo está actuando el filtro? Comenta tus conclusiones.
En este caso el filtro es un paso bajo, por lo que elimina los cambios mas bruscos. La onda cuadrada contiene cambios muy bruscos, por lo que al suavizarlos, la transforma en lo que vemos en la primera imagen. Respecto a las dos restantes, vemos como actúa el filtro en frecuencia, conservando la energía en las frecuencias bajas y reduciéndola en las frecuencias altas.
¿Cómo colocarías R y C para hacer un filtro paso alto?
En posiciones inversas a las de este esquema, en primer lugar el condensador y después la resistencia.