Diferencia entre revisiones de «2. Movimiento ondulatorio. Ondas.»
| (No se muestran 55 ediciones intermedias del mismo usuario) | |||
| Línea 7: | Línea 7: | ||
* Tipos de ondas | * Tipos de ondas | ||
** Onda viajera: Si la perturbación es una onda viajera alcanza al cabo de un tiempo todos los puntos del medio. (ej: piedra en estanque) | ** Onda viajera: Si la perturbación es una onda viajera alcanza al cabo de un tiempo todos los puntos del medio. (ej: piedra en estanque) | ||
** Onda estacionaria: Es estacionaria cuando la propagación esta delimitada mediante fronteras a una | ** Onda estacionaria: Es estacionaria cuando la propagación esta delimitada mediante fronteras a una región especifica del medio. (ej: cuerda de guitarra) | ||
Pulso de onda: Es una perturbación individual que se propaga a través de un medio. | Pulso de onda: Es una perturbación individual que se propaga a través de un medio. | ||
| Línea 25: | Línea 25: | ||
*Ondas transversales: Cuando la dirección de propagación y la de vibración son perpendiculares. | *Ondas transversales: Cuando la dirección de propagación y la de vibración son perpendiculares. | ||
[[File:Onda-longitudinal.png|center|400px]] | |||
*Ondas longitudinales: Si la dirección de propagación coincide con la dirección de vibración. Es una sucesión de contracciones y dilataciones del medio. | *Ondas longitudinales: Si la dirección de propagación coincide con la dirección de vibración. Es una sucesión de contracciones y dilataciones del medio. | ||
=== Dependiendo del numero de dimensiones en las que se propaga la | === Dependiendo del numero de dimensiones en las que se propaga la energía de la onda=== | ||
*Ondas unidimensionales: Se propaga en una dimensión (ej: cuerda) | *Ondas unidimensionales: Se propaga en una dimensión (ej: cuerda) | ||
| Línea 37: | Línea 38: | ||
Sea una onda que se transmite por una cuerda. | Sea una onda que se transmite por una cuerda. | ||
[[File:Ondas-armonicas.jpg|300px|center]] | |||
* Amplitud (A): Es la máxima amplitud con la que vibran las partículas del medio donde se desplaza la onda. Depende solo de la energía que se propaga. (unidades: m) | * Amplitud (A): Es la máxima amplitud con la que vibran las partículas del medio donde se desplaza la onda. Depende solo de la energía que se propaga. (unidades: m) | ||
| Línea 57: | Línea 60: | ||
== Ecuación de las ondas armónicas unidimensionales== | == Ecuación de las ondas armónicas unidimensionales== | ||
[[File:2.3.1.png]] | |||
Se define la ecuación de una onda como la expresión matemática que permite obtener la elongación y de una partícula en un instante t. | Se define la ecuación de una onda como la expresión matemática que permite obtener la elongación y de una partícula en un instante t. | ||
| Línea 68: | Línea 73: | ||
<center><math>y(0,0) = A cos (0 + \varphi_0)=0</math></center> | <center><math>y(0,0) = A cos (0 + \varphi_0)=0</math></center> | ||
<center>Para que dicha | <center>Para que dicha ecuación sea cierta, <math>cos \varphi_0 = 1 \Rightarrow \varphi_0 = 0</math></center> | ||
<center>En todo t=t comprobamos que: </center> | <center>En todo t=t comprobamos que: </center> | ||
<center> | |||
<center> | <center><math>y (0, t) =A cos (\omega t+0)</math></center> | ||
<center> | |||
<center> | <center>Aplicamos <math>\omega = 2 \pi f</math></center> | ||
<center> | |||
<center> | <center>Para todo t=t en x podemos decir que:</center> | ||
<center> | |||
<center> | <center><math>y (x,t) = A cos [2 \pi f (t+t')]</math></center> | ||
<center>Siendo t' el retraso. Aplicamos <math>v = \frac {x}{t'}</math></center> | |||
<center><math>y (x,t) = A cos [2 \pi f (t+\frac {x}{v})]</math></center> | |||
<center>Aplicamos <math>v = \frac {\lambda}{T}= \lambda f</math> y sacamos factor comun:</center> | |||
<center><math>y (x,t) = A cos [2 \pi( ft-\frac {fx}{f\lambda})] = A cos [2 \pi ft- 2 \pi \frac {x}{\lambda})]</math></center> | |||
<center>Aplicamos <math>k = \frac {2\pi}{\lambda}</math></center> | |||
<center><math>y (x,t) = A cos (2 \pi ft- kx)</math></center> | |||
<center>Aplicamos <math>\omega = 2 \pi f</math> y simplificamos para obtener la '''ecuacion de la onda armonica transversal y unidireccional''' </center> | |||
<center><math>y (x,t) = A cos (\omega t - kx)</math></center> | |||
Si la onda se propaga en el eje OX en sentido positivo, la ecuacion es: | |||
<math>y (x,t) = A cos (\omega t - kx)</math> | |||
Si la onda se propaga en el eje OX en sentido negativo, la ecuacion es: | |||
<math>y (x,t) = A cos (\omega t + kx)</math> | |||
Generalizando las ecuanciones y teniendo en cuenta que <math>\varphi_0</math> puede ser distinto de 0: | |||
<math>y (x,t) = A cos (\omega t \pm kx + \varphi_0)</math> | |||
La velocidad de la particula en ese punto será: | |||
<math>v (x,t) = \frac {dy (x,t)}{dt} = -A \omega sin (\omega t \pm kx + \varphi_0)</math> | |||
La aceleracion de la particula en ese punto será: | |||
<math>v (x,t) = \frac {dv (x,t)}{dt} = -A \omega^2 cos (\omega t \pm kx + \varphi_0)</math> | |||
==Puntos de fase y de oposición de fase de una onda== | ==Puntos de fase y de oposición de fase de una onda== | ||
| Línea 84: | Línea 125: | ||
Sea una onda armónica unidimensional y transversal, avanzando según el sentido positivo del eje OX | Sea una onda armónica unidimensional y transversal, avanzando según el sentido positivo del eje OX | ||
[[File:Onda-1.PNG|center]] | |||
y(x,t) = A cos | <math>y(x,t) = A cos(\omega t - kx - \varphi_0)</math> donde <math>(\omega t - kx - \varphi_0) \Rightarrow \delta</math> (fase de onda) | ||
Se dice que dos puntos x<sub>1</sub> y x<sub>2</sub> | Se dice que dos puntos x<sub>1</sub> y x<sub>2</sub> están en fase, es decir, tienen el mismo estado de vibración, si la diferencia de fase entre ellos es un numero par de veces π. | ||
<center>x<sub>1</sub>, x<sub>2</sub> ⇒ fase ⇒ nº par veces π</center> | <center>x<sub>1</sub>, x<sub>2</sub> ⇒ fase ⇒ nº par veces π</center> | ||
<center>En fase: | <center>En fase: <math>\Delta\delta = 2n\pi, n\in \mathbb Z</math></center> | ||
En el instante t: <math>\delta_1 = \omega t - kx_1 - \varphi_0</math> y <math>\delta_2 = \omega t - kx_2 - \varphi_0</math> | |||
<math>\Delta\delta = \delta_2-\delta_1 = (\omega t - kx_2 - \varphi_0)-(\omega t - kx_1 - \varphi_0) = kx_1-kx_2 = k(x_1-x_2) = 2n\pi , n\in \mathbb Z</math> | |||
<math>\Delta\delta = k(x_1-x_2) = 2n\pi</math> | |||
Aplicando <math>k=\frac {2\pi}{\lambda}</math> | |||
<math>\frac {2\pi}{\lambda}(x_1-x_2) = 2n\pi \Rightarrow |x_1-x_2| = n\lambda , n\in \mathbb Z</math> | |||
Se dice que dos puntos x<sub>1</sub> y x<sub>2</sub> están en oposición de fase si la diferencia de fase entre ellos es un numero impar de veces π. | Se dice que dos puntos x<sub>1</sub> y x<sub>2</sub> están en oposición de fase si la diferencia de fase entre ellos es un numero impar de veces π. | ||
[[File:2.6.2.png|center|400px]] | |||
<center><math>\Delta\delta = (2n+1)\pi, n\in \mathbb Z</math></center> | |||
<math>\Delta\delta = \delta_2-\delta_1 = (\omega t - kx_2 - \varphi_0 )-(\omega t - kx_1 - \varphi_0 ) \Rightarrow \Delta\delta = k(x_1-x_2) = (2n+1)\pi </math> | |||
< | Aplicamos <math>k=\frac {2\pi} {\lambda} </math> | ||
<math>\Delta\delta = \frac {2\pi} {\lambda} (x_1-x_2) = (2n+1)\pi \Rightarrow |x_1-x_2| = (2n+1) \lambda /2, n\in \mathbb Z</math> | |||
Todos los demas puntos de x<sub>1</sub> y x<sub>2</sub> que no verifican las condiciones anteriores se dice que están en desfase. | Todos los demas puntos de x<sub>1</sub> y x<sub>2</sub> que no verifican las condiciones anteriores se dice que están en desfase. | ||
| Línea 118: | Línea 167: | ||
Demostración: | Demostración: | ||
<math>y(x,t) = A cos(\omega t - kx)</math>;<math>y(x,t+nT) = A cos[\omega (t+nT) - kx]</math> | <center><math>y(x,t) = A cos(\omega t - kx)</math>;<math>y(x,t+nT) = A cos[\omega (t+nT) - kx]</math> </center> | ||
<center><math>y(x,t+nT) = A cos[\omega(t+nT) - kx] = A cos(\omega t + \omega nT - kx)</math></center> | <center><math>y(x,t+nT) = A cos[\omega(t+nT) - kx] = A cos(\omega t + \omega nT - kx)</math></center> | ||
| Línea 141: | Línea 190: | ||
"""Dibujo de una onda con puntos x+nλ con imágenes y coincidentes""" | """Dibujo de una onda con puntos x+nλ con imágenes y coincidentes""" | ||
y(x,t) = y(x+ | <math>y(x,t) = y(x+n\lambda ,t), n\in Z</math> | ||
Demostración: | Demostración: | ||
y(x,t) = A cos( | <center><math>y(x,t) = A cos(2\pi ft - kx)</math> ; <math>y(x+n\lambda ,t) = A cos[2\pi ft - k(x+n\lambda )]</math></center> | ||
y(x+ | |||
<center><math>y(x+n\lambda ,t) = A cos[2\pi ft - k(x+n\lambda )] = A cos(2\pi ft - kx - kn\lambda )</math> </center> | |||
<center>Aplicamos <math>k=\frac{2\pi}{\lambda}</math></center> | |||
<center><math>A cos(2\pi ft - kx - (\frac{2\pi}{\lambda})n\lambda ) = A cos(2\pi ft - kx - 2\pi n)</math> </center> | |||
<center>Aplicamos <math>cos\alpha =cos\alpha +2n\pi</math></center> | |||
<center><math>A cos(2\pi ft - kx) = y(x,t)</math></center> | |||
==Propiedades de las ondas== | |||
Ciertos fenomenos ondulatorios, como la reflexion, la refraccion y la difraccion, tienen una explicacion sencilla utilizando un metodo geometrico planteado por Huygens en el siglo XVII | |||
Esta explicacion es valida para cualquier tipo de ondas, y permite explicar como se propaga una onda, o lo que es lo mismo, como lo hace la energia en un medio dado | |||
Ejemplo: Onda electromagnetica tridimensional | |||
[[File:Onda electronagnetica tridimensional.png|100px|left]]Sea una onda electromagnetica con infinitos frentes de onda de superficie esferica y con todos sus puntos en fase. | |||
Como los frentes de onda son superficies esfericas, se habla de ondas esfericas. Las direcciones de propagacion de la energia se denominan rayos. | |||
Si el medio donde se propaga la onda es homogeneo, de densidad constante, e isotropo, de caracteristicas iguales; la direccion de propagacion de los rayos es siempre perpendicular a los frentes de onda. | |||
Ejemplo: Onda electromagnetica bidimensional | |||
[[File:Onda 01.gif]] | |||
===Principio de Huygens=== | |||
Frente de ondas es el lugar geometrico del espacio donde todos los puntos en un instante dado estan en fase. | |||
Todo punto en un frente de ondas es centro emisor de nuevas ondas elementales cuyo envolvente es el nuevo frente de ondas | |||
[[File:Onda huygens.gif]] | |||
Cuanto mas se aleje la onda llegará un momento en que los frentes de onda sean rectos. | |||
===Estudio cualitativo de algunas propiedades de las ondas.=== | |||
Cuando un movimiento ondulatorio que se propaga por un medio alcanza la superficie que le separa de otro mediode distinta naturaleza, parte de la energia es devuelta al medio de procedencia , es decir, tiene lugar la reflesion de la onda. Al mismo tiempo, otra parte de la energia de la onda incidente se transmite al segundo medio. | |||
[[File:O6.gif]] | |||
====Reflexion==== | |||
Es un fenomeno propio de cualquier tipo de ondas, y puede ser explicado mediante el principio de Huygens. Se define como el cambio de direccion de propagacion de una onda cuando incide sobre una superficie reflectante. La superficie reflectante suele ser una superficie de separacion entre dos medios. | |||
[[File:Refexion.png]] | |||
La reflexion de las ondas cumple las leyes de Snell: | |||
# que el angulo <math>\hat{i}</math> y <math>\hat{r}</math> son iguales. | |||
# que los rayos incidente y reflejado estan en el mismo plano. | |||
====Refraccion==== | |||
Llamamos refraccion al fenomeno por el cual al llegar una onda a la superficie de separacion de dos medios, penetra y se transmite en el segundo de ellos, junto con una parte de la energia del movimiento ondulatorio, cambiando su direccion. | |||
[[File:Refraccion.png|200px]] | |||
Ley de Snell: <math>\frac {sin \hat{i}}{sin \hat{r}} = \frac {v_1}{v_2}</math> | |||
====Difraccion==== | |||
Fenomeno ondulatorio que se produce cuandp im obstaculo impide el avance de una parte del frente de ondas. | |||
[[File:Difaccion.png|200px]] | |||
Los puntos que no estan tapados por el obstaculo se convierten en meros centros emisores de nuevos frentes de onda. | |||
====Polarizacion==== | |||
Decimos que una onda no esta polarizada cuando son igualmente posibles todas las direcciones de oscilacion de las particulas del medio a lo largo del tiempo, o bien, cuando la onda esta formada por la superposicion de muchas ondas cuyas vibraciones tienen lugar en distintas direcicones. | |||
[[File:Luz polarizada.png|150px]] | |||
De lo contrario, hablamos de ondas polarizadas. | |||
Polarizador: Dispositivo que permite la transmision de una onda en una direccion de vibracion elegida. | |||
Solo las ondas tranversales son polarizables. | |||
[[File:Hoja.png|1200px]] | |||
====Interferecias de ondas==== | |||
Sean dos ondas emitidas por focos distintos que se propagan por el mismo medio y que se superponen en un mismo punto P. Esta superposicion recibe el nombre de interferencia. El caso mas importante es cuando las ondas que interfieren son coherentes, tienen las mismas caracteristicas. | |||
=====Principio de Superposicion===== | |||
Para estudiar la interferencia de ondas nos basamos en el principio de superposicion. | |||
[[File:Interferencias.png|200px]] x<sub>1</sub> = distancia respecto a F<sub>1</sub>; x<sub>2</sub> = distancia respecto a F<sub>2</sub> | |||
Sean dos ondas coherentes propagandose por el mismo medio producidos por focos emisores diferentes que se superponen en un punto P segun la figura. | |||
Las ecuaciones de onda de dichas ondas vienen dadas por: | |||
<math>y_1 (x_1, t) =A cos (\omega t - k x_1)</math> | |||
<math>y_2 (x_2, t) =A cos (\omega t - k x_2)</math> | |||
Segun el principio de superposicion, la onda resultante será: <math>y = y_1 + y_2</math> | |||
<math>y = y_1 + y_2 = A cos (2\pi f t - k x_1 + A cos (2\pi f t - k x_2</math> | |||
Sacando factor comun, obtenemos <math> A [cos (2\pi f t - k x_1) + cos (2\pi f t - k x_2)]</math> | |||
Aplicando el principio trigonometrico <math>cos \alpha + cos \beta = 2 [cos {\frac{(\alpha + \beta)}{2}][cos {\frac{(\alpha - \beta)}{2}]</math> obtenemos: | |||
<math>2 A cos [\frac {(2\pi f t - k x_1 + 2\pi f t - k x_2)}{2}] cos [\frac {(2\pi f t - k x_1 - 2\pi f t - k x_2)}{2}]=</math> | |||
<math>= 2 A cos [\frac {4\pi f t}{2} - \frac {k (x_1 - x_2)} {2}] cos [{\frac {k}{2}} (x_1 - x_2)]</math> | |||
Donde <math>2 A cos [{\frac {k}{2}} (x_1 - x_2)] = A_r</math> | |||
Por tanto, concluimos que <math>y= A_r cos [2\pi f t - \frac {k (x_1 - x_2)} {2}]</math> | |||
Por su parte, <math>A_r = 2 A cos [{\frac {k}{2}} (x_1 - x_2)]</math> podemos tomarlo como <math>A_r = 2 A cos [{\frac {2\pi}{2\lambda}} (x_1 - x_2)]</math> aplicando <math>k = \frac {2\pi}{\lambda}</math>, que simplificando queda como <math>A_r = 2 A cos [{\frac {\pi}{\lambda}} (x_1 - x_2)]</math> | |||
Por lo tanto, la onda resultante tiene la misma frecuencia y longitud de onda que la onda incidente, y su amplitud será <math>A_r</math>, que depende de la posicion de los focos emisores. | |||
La <math>A_r</math> puede tomar diferentes valores atendiendo a la diferencia de caminos seguidos por las ondas para alcanzar el punto P | |||
=====Interferencia constructiva===== | |||
Se dice que en P hay una interferencia constructiva cuando la onda resultante tiene un valor de <math>A_r =2A</math>. | |||
En ese momento, el coseno de <math>A_r</math> será 1, y se dará cuando <math>\frac {\pi}{\lambda}(x_2-x_1) = n\pi , n \in \mathbb Z</math>, es decir, <math>(x_2-x_1) = n\lambda , n \in \mathbb Z</math> | |||
Ocurrirá en todos los puntos en los que las diferencias de distancias a los focos sean un nuemro entero de longitudes de onda. | |||
=====Interferencia destructiva===== | |||
Se dice que en P hay una interferencia destructiva cuando la onda resultante tiene un a amplitud 0. | |||
En ese momento, el coseno de <math>A_r</math> será 0, y se dará cuando <math>\frac {\pi}{\lambda}(x_2-x_1) = (2n-1) \frac{\pi}{2} , n \in \mathbb Z</math>, es decir, <math>(x_2-x_1) = (2n-1) \frac{\lambda}{2} , n \in \mathbb Z</math> | |||
Las ondas llegaran en oposicion de fase en todos aquellos puntos en los que la diferencia de distancia sea un numero impar de longitudes de onda. | |||
==Transmision de energia a traves de un medio== | |||
Una onda armonica transmite la energia de un oscilador armonico. Suponemos una particula de masa m situada en el origen de coordenadas con movimiento armonico simple. Esta particula será el oscilador cuya energia viene dada por: | |||
[[File:2.8.png|200px]] | |||
Esta energia se irradia en todas las direcciones en forma de ondas esfericas con velocidad v si el medio es homogeneo e isotropo. | |||
Consideramos ahora la energia que poseen las particulas situadas dentro de una superficie esferica de radio r y espesor <math>dr_1</math> o <math>dE</math>. La masa contenida en ese espesor la llamaremos dm, y sea <math>A_1</math> la amplitud de las particulas en el frente <math>F_1</math>. | |||
==Ondas estacionarias== | |||
Hasta ahora hemos estudiado ondas que se propagan en un medio abierto, es decir, la propagacion no encuentra ningun obstaculo que refleje las ondas hacia la fuente emisora. | |||
Cuando un tren de ondas se encuentra con una frontera, la parte reflejada interfiere con la incidente, y se originan las ondas estacionarias. | |||
[[Archivo:Ondaes1.gif|center]] | |||
<center><math>y_1 (x,t)=A cos (2\pi ft-kx)</math></center> | |||
<center><math>y_2 (x,t)=-A cos (2\pi ft-kx)</math></center> | |||
Las ondas estacionarias reciben este nombre porque el perfil de la onda no se desplaza, debido a que existen puntos fijos. (nodos y vientres) | |||
Revisión actual del 09:31 8 nov 2013
Temario de Fisica (2012-2013)
Definiciones
Onda: Una onda es la propagación de energía sin que haya desplazamiento de materia. Cuando una onda se propaga, las partículas del medio no acompañan el movimiento de avance de la onda. Para que se produzca un movimiento ondulatorio, se necesita una fuente de energía o centro emisor que produzca una perturbación. También puede existir, en algunos casos, un medio que la transmita.
- Tipos de ondas
- Onda viajera: Si la perturbación es una onda viajera alcanza al cabo de un tiempo todos los puntos del medio. (ej: piedra en estanque)
- Onda estacionaria: Es estacionaria cuando la propagación esta delimitada mediante fronteras a una región especifica del medio. (ej: cuerda de guitarra)
Pulso de onda: Es una perturbación individual que se propaga a través de un medio.
Tren de ondas: Es la propagación de una perturbación continua. Todos los puntos del medio están en movimiento. Es necesario suministrar energía continuamente. Cada punto de la cuerda posee un movimiento armónico simple.
Tipos de ondas
Se clasifican según diferentes criterios.
Según el tipo de energía con que se propagan
- Ondas mecánicas: Se propagan con energía mecánica y necesitan de un medio material de propagación. (ej: cuerda)
- Ondas electromagnéticas: La energía propagada es energía electromagnética, producida por oscilaciones de cargas eléctricas aceleradas. Dichas ondas no necesitan de un medio material para propagarse. (ej: luz)
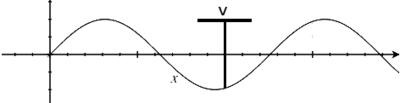
Relación entre la dirección de propagación y la dirección de vibración
- Ondas transversales: Cuando la dirección de propagación y la de vibración son perpendiculares.
- Ondas longitudinales: Si la dirección de propagación coincide con la dirección de vibración. Es una sucesión de contracciones y dilataciones del medio.
Dependiendo del numero de dimensiones en las que se propaga la energía de la onda
- Ondas unidimensionales: Se propaga en una dimensión (ej: cuerda)
- Ondas bidimensionales: Se propaga en dos dimensiones (ej: superficie del agua)
- Ondas tridimensionales: Se propaga en tres dimensiones (ej; ondas de radio)
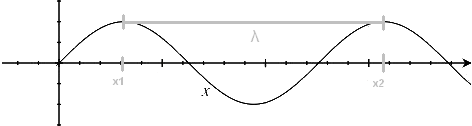
Magnitudes características de las ondas armónicas
Sea una onda que se transmite por una cuerda.
- Amplitud (A): Es la máxima amplitud con la que vibran las partículas del medio donde se desplaza la onda. Depende solo de la energía que se propaga. (unidades: m)
- Longitud de onda (λ): Es la distancia mínima entre dos puntos consecutivos que se hallan en el mismo estado de vibración. (unidades: m)
- Periodo (T): Tiempo que tarda un punto cualquiera en hacer una oscilación completa. T=1/f (unidades: s)
- Frecuencia de onda (f): Indica el numero de oscilaciones completas que pasan por un medio en un segundo (unidades: Hz)
- Puntos en fase: Se dice que dos puntos de una onda están en fase si tienen el mismo estado de vibración. Si tienen estados de vibración opuestos, se dice que están en oposición de fase.
- Velocidad de propagación (v): También se denomina velocidad de fase. Es la misma en todas las direcciones. (unidades: m/s)
[math]\displaystyle{ v=\frac{\lambda}{T}=\lambda f }[/math]
Su valor en las ondas electromagneticas es de [math]\displaystyle{ v_{electr}=3\cdot 10^8 m/s }[/math]
- Numero de onda (k): representa el numero de longitudes de onda en una distancia 2π (unidades: m-1)
[math]\displaystyle{ k=\frac{2\pi}{\lambda} }[/math] - Relacion de otras magnitudes con el numero de onda: Teniendo en cuenta que
- Fase de la onda (δ): Informa sobre el estado de vibración de una partícula x de la onda en cualquier instante t (unidades: rad)
- Constante de fase (φ0): Se determina a partir de las condiciones iniciales (unidades: rad)
Ecuación de las ondas armónicas unidimensionales
Se define la ecuación de una onda como la expresión matemática que permite obtener la elongación y de una partícula en un instante t.
Cada punto de la cuerda alcanzado por la perturbación posee un movimiento armónico simple y, por tanto, el estado de vibracion de la partícula en el instante t vendrá dado por la siguiente ecuación:
Si la onda se propaga en el eje OX en sentido positivo, la ecuacion es:
[math]\displaystyle{ y (x,t) = A cos (\omega t - kx) }[/math]
Si la onda se propaga en el eje OX en sentido negativo, la ecuacion es:
[math]\displaystyle{ y (x,t) = A cos (\omega t + kx) }[/math]
Generalizando las ecuanciones y teniendo en cuenta que [math]\displaystyle{ \varphi_0 }[/math] puede ser distinto de 0:
[math]\displaystyle{ y (x,t) = A cos (\omega t \pm kx + \varphi_0) }[/math]
La velocidad de la particula en ese punto será:
[math]\displaystyle{ v (x,t) = \frac {dy (x,t)}{dt} = -A \omega sin (\omega t \pm kx + \varphi_0) }[/math]
La aceleracion de la particula en ese punto será:
[math]\displaystyle{ v (x,t) = \frac {dv (x,t)}{dt} = -A \omega^2 cos (\omega t \pm kx + \varphi_0) }[/math]
Puntos de fase y de oposición de fase de una onda
Sea una onda armónica unidimensional y transversal, avanzando según el sentido positivo del eje OX
[math]\displaystyle{ y(x,t) = A cos(\omega t - kx - \varphi_0) }[/math] donde [math]\displaystyle{ (\omega t - kx - \varphi_0) \Rightarrow \delta }[/math] (fase de onda)
Se dice que dos puntos x1 y x2 están en fase, es decir, tienen el mismo estado de vibración, si la diferencia de fase entre ellos es un numero par de veces π.
En el instante t: [math]\displaystyle{ \delta_1 = \omega t - kx_1 - \varphi_0 }[/math] y [math]\displaystyle{ \delta_2 = \omega t - kx_2 - \varphi_0 }[/math]
[math]\displaystyle{ \Delta\delta = \delta_2-\delta_1 = (\omega t - kx_2 - \varphi_0)-(\omega t - kx_1 - \varphi_0) = kx_1-kx_2 = k(x_1-x_2) = 2n\pi , n\in \mathbb Z }[/math]
[math]\displaystyle{ \Delta\delta = k(x_1-x_2) = 2n\pi }[/math]
Aplicando [math]\displaystyle{ k=\frac {2\pi}{\lambda} }[/math]
[math]\displaystyle{ \frac {2\pi}{\lambda}(x_1-x_2) = 2n\pi \Rightarrow |x_1-x_2| = n\lambda , n\in \mathbb Z }[/math]
Se dice que dos puntos x1 y x2 están en oposición de fase si la diferencia de fase entre ellos es un numero impar de veces π.
[math]\displaystyle{ \Delta\delta = \delta_2-\delta_1 = (\omega t - kx_2 - \varphi_0 )-(\omega t - kx_1 - \varphi_0 ) \Rightarrow \Delta\delta = k(x_1-x_2) = (2n+1)\pi }[/math]
Aplicamos [math]\displaystyle{ k=\frac {2\pi} {\lambda} }[/math]
[math]\displaystyle{ \Delta\delta = \frac {2\pi} {\lambda} (x_1-x_2) = (2n+1)\pi \Rightarrow |x_1-x_2| = (2n+1) \lambda /2, n\in \mathbb Z }[/math]
Todos los demas puntos de x1 y x2 que no verifican las condiciones anteriores se dice que están en desfase.
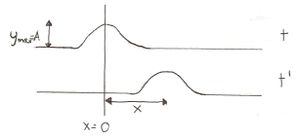
Propiedades básicas de una onda transversal unidireccional
La ecuación de una onda armónica es doblemente periódica.
Periódica respecto del tiempo t
[math]\displaystyle{ y(x,t) = y(x,t+nT), n\in \mathbb Z }[/math]
Demostración:
Periódica respecto del espacio x
La vibración y de la partícula se repite en aquellos puntos cuyas distancias x son múltiplos de la longitud de onda.
"""Dibujo de una onda con puntos x+nλ con imágenes y coincidentes"""
[math]\displaystyle{ y(x,t) = y(x+n\lambda ,t), n\in Z }[/math]
Demostración:
Propiedades de las ondas
Ciertos fenomenos ondulatorios, como la reflexion, la refraccion y la difraccion, tienen una explicacion sencilla utilizando un metodo geometrico planteado por Huygens en el siglo XVII
Esta explicacion es valida para cualquier tipo de ondas, y permite explicar como se propaga una onda, o lo que es lo mismo, como lo hace la energia en un medio dado
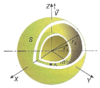
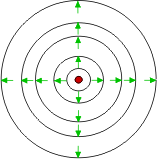
Ejemplo: Onda electromagnetica tridimensional
Sea una onda electromagnetica con infinitos frentes de onda de superficie esferica y con todos sus puntos en fase.
Como los frentes de onda son superficies esfericas, se habla de ondas esfericas. Las direcciones de propagacion de la energia se denominan rayos.
Si el medio donde se propaga la onda es homogeneo, de densidad constante, e isotropo, de caracteristicas iguales; la direccion de propagacion de los rayos es siempre perpendicular a los frentes de onda.
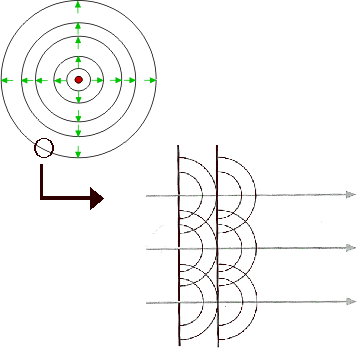
Ejemplo: Onda electromagnetica bidimensional
Principio de Huygens
Frente de ondas es el lugar geometrico del espacio donde todos los puntos en un instante dado estan en fase.
Todo punto en un frente de ondas es centro emisor de nuevas ondas elementales cuyo envolvente es el nuevo frente de ondas
Cuanto mas se aleje la onda llegará un momento en que los frentes de onda sean rectos.
Estudio cualitativo de algunas propiedades de las ondas.
Cuando un movimiento ondulatorio que se propaga por un medio alcanza la superficie que le separa de otro mediode distinta naturaleza, parte de la energia es devuelta al medio de procedencia , es decir, tiene lugar la reflesion de la onda. Al mismo tiempo, otra parte de la energia de la onda incidente se transmite al segundo medio.
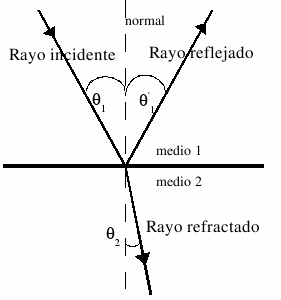
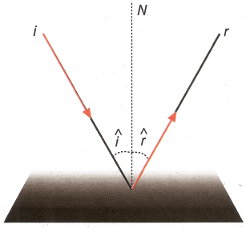
Reflexion
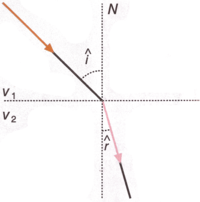
Es un fenomeno propio de cualquier tipo de ondas, y puede ser explicado mediante el principio de Huygens. Se define como el cambio de direccion de propagacion de una onda cuando incide sobre una superficie reflectante. La superficie reflectante suele ser una superficie de separacion entre dos medios.
La reflexion de las ondas cumple las leyes de Snell:
- que el angulo [math]\displaystyle{ \hat{i} }[/math] y [math]\displaystyle{ \hat{r} }[/math] son iguales.
- que los rayos incidente y reflejado estan en el mismo plano.
Refraccion
Llamamos refraccion al fenomeno por el cual al llegar una onda a la superficie de separacion de dos medios, penetra y se transmite en el segundo de ellos, junto con una parte de la energia del movimiento ondulatorio, cambiando su direccion.
Ley de Snell: [math]\displaystyle{ \frac {sin \hat{i}}{sin \hat{r}} = \frac {v_1}{v_2} }[/math]
Difraccion
Fenomeno ondulatorio que se produce cuandp im obstaculo impide el avance de una parte del frente de ondas.
Los puntos que no estan tapados por el obstaculo se convierten en meros centros emisores de nuevos frentes de onda.
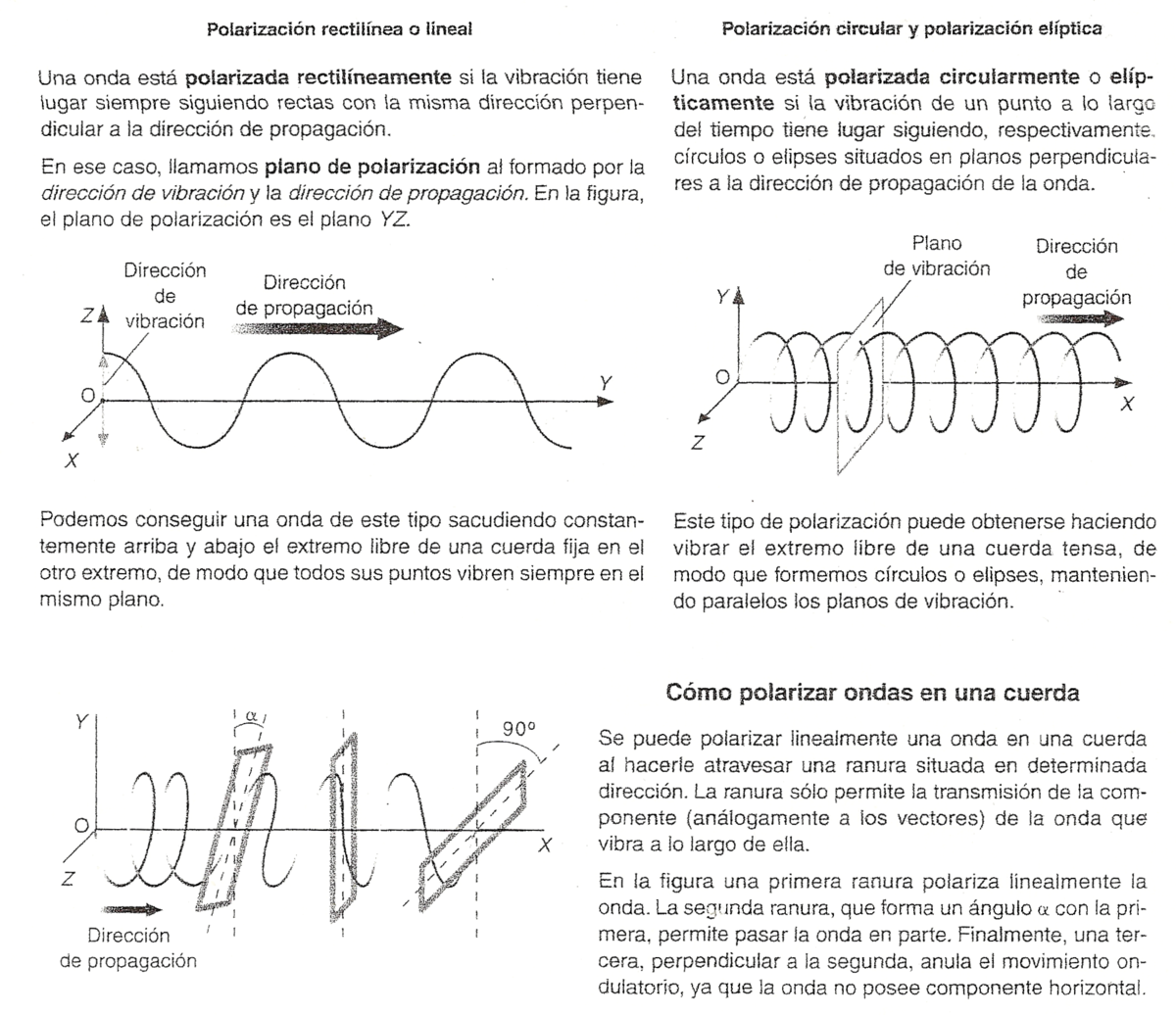
Polarizacion
Decimos que una onda no esta polarizada cuando son igualmente posibles todas las direcciones de oscilacion de las particulas del medio a lo largo del tiempo, o bien, cuando la onda esta formada por la superposicion de muchas ondas cuyas vibraciones tienen lugar en distintas direcicones.
De lo contrario, hablamos de ondas polarizadas.
Polarizador: Dispositivo que permite la transmision de una onda en una direccion de vibracion elegida.
Solo las ondas tranversales son polarizables.
Interferecias de ondas
Sean dos ondas emitidas por focos distintos que se propagan por el mismo medio y que se superponen en un mismo punto P. Esta superposicion recibe el nombre de interferencia. El caso mas importante es cuando las ondas que interfieren son coherentes, tienen las mismas caracteristicas.
Principio de Superposicion
Para estudiar la interferencia de ondas nos basamos en el principio de superposicion.
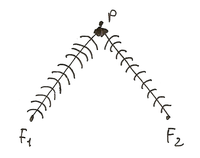 x1 = distancia respecto a F1; x2 = distancia respecto a F2
x1 = distancia respecto a F1; x2 = distancia respecto a F2
Sean dos ondas coherentes propagandose por el mismo medio producidos por focos emisores diferentes que se superponen en un punto P segun la figura.
Las ecuaciones de onda de dichas ondas vienen dadas por:
[math]\displaystyle{ y_1 (x_1, t) =A cos (\omega t - k x_1) }[/math]
[math]\displaystyle{ y_2 (x_2, t) =A cos (\omega t - k x_2) }[/math]
Segun el principio de superposicion, la onda resultante será: [math]\displaystyle{ y = y_1 + y_2 }[/math]
[math]\displaystyle{ y = y_1 + y_2 = A cos (2\pi f t - k x_1 + A cos (2\pi f t - k x_2 }[/math]
Sacando factor comun, obtenemos [math]\displaystyle{ A [cos (2\pi f t - k x_1) + cos (2\pi f t - k x_2)] }[/math]
Aplicando el principio trigonometrico [math]\displaystyle{ cos \alpha + cos \beta = 2 [cos {\frac{(\alpha + \beta)}{2}][cos {\frac{(\alpha - \beta)}{2}] }[/math] obtenemos:
[math]\displaystyle{ 2 A cos [\frac {(2\pi f t - k x_1 + 2\pi f t - k x_2)}{2}] cos [\frac {(2\pi f t - k x_1 - 2\pi f t - k x_2)}{2}]= }[/math]
[math]\displaystyle{ = 2 A cos [\frac {4\pi f t}{2} - \frac {k (x_1 - x_2)} {2}] cos [{\frac {k}{2}} (x_1 - x_2)] }[/math]
Donde [math]\displaystyle{ 2 A cos [{\frac {k}{2}} (x_1 - x_2)] = A_r }[/math]
Por tanto, concluimos que [math]\displaystyle{ y= A_r cos [2\pi f t - \frac {k (x_1 - x_2)} {2}] }[/math]
Por su parte, [math]\displaystyle{ A_r = 2 A cos [{\frac {k}{2}} (x_1 - x_2)] }[/math] podemos tomarlo como [math]\displaystyle{ A_r = 2 A cos [{\frac {2\pi}{2\lambda}} (x_1 - x_2)] }[/math] aplicando [math]\displaystyle{ k = \frac {2\pi}{\lambda} }[/math], que simplificando queda como [math]\displaystyle{ A_r = 2 A cos [{\frac {\pi}{\lambda}} (x_1 - x_2)] }[/math]
Por lo tanto, la onda resultante tiene la misma frecuencia y longitud de onda que la onda incidente, y su amplitud será [math]\displaystyle{ A_r }[/math], que depende de la posicion de los focos emisores.
La [math]\displaystyle{ A_r }[/math] puede tomar diferentes valores atendiendo a la diferencia de caminos seguidos por las ondas para alcanzar el punto P
Interferencia constructiva
Se dice que en P hay una interferencia constructiva cuando la onda resultante tiene un valor de [math]\displaystyle{ A_r =2A }[/math].
En ese momento, el coseno de [math]\displaystyle{ A_r }[/math] será 1, y se dará cuando [math]\displaystyle{ \frac {\pi}{\lambda}(x_2-x_1) = n\pi , n \in \mathbb Z }[/math], es decir, [math]\displaystyle{ (x_2-x_1) = n\lambda , n \in \mathbb Z }[/math]
Ocurrirá en todos los puntos en los que las diferencias de distancias a los focos sean un nuemro entero de longitudes de onda.
Interferencia destructiva
Se dice que en P hay una interferencia destructiva cuando la onda resultante tiene un a amplitud 0.
En ese momento, el coseno de [math]\displaystyle{ A_r }[/math] será 0, y se dará cuando [math]\displaystyle{ \frac {\pi}{\lambda}(x_2-x_1) = (2n-1) \frac{\pi}{2} , n \in \mathbb Z }[/math], es decir, [math]\displaystyle{ (x_2-x_1) = (2n-1) \frac{\lambda}{2} , n \in \mathbb Z }[/math]
Las ondas llegaran en oposicion de fase en todos aquellos puntos en los que la diferencia de distancia sea un numero impar de longitudes de onda.
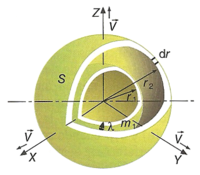
Transmision de energia a traves de un medio
Una onda armonica transmite la energia de un oscilador armonico. Suponemos una particula de masa m situada en el origen de coordenadas con movimiento armonico simple. Esta particula será el oscilador cuya energia viene dada por:
Esta energia se irradia en todas las direcciones en forma de ondas esfericas con velocidad v si el medio es homogeneo e isotropo.
Consideramos ahora la energia que poseen las particulas situadas dentro de una superficie esferica de radio r y espesor [math]\displaystyle{ dr_1 }[/math] o [math]\displaystyle{ dE }[/math]. La masa contenida en ese espesor la llamaremos dm, y sea [math]\displaystyle{ A_1 }[/math] la amplitud de las particulas en el frente [math]\displaystyle{ F_1 }[/math].
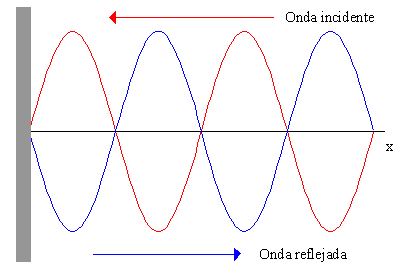
Ondas estacionarias
Hasta ahora hemos estudiado ondas que se propagan en un medio abierto, es decir, la propagacion no encuentra ningun obstaculo que refleje las ondas hacia la fuente emisora.
Cuando un tren de ondas se encuentra con una frontera, la parte reflejada interfiere con la incidente, y se originan las ondas estacionarias.
Las ondas estacionarias reciben este nombre porque el perfil de la onda no se desplaza, debido a que existen puntos fijos. (nodos y vientres)