Diferencia entre revisiones de «3. Ley de la Gravitacion Universal»

Pertenece a Fisica (2012-2013)

Antecedentes

Existen dos modelos de movimiento en el universo. El modelo geocentrico es el mas antiguo, y situa a la tierra en el centro del universo. Dicho modelo se descartó, pasando al modelo heliocentrico. Este modelo, popularizado por Copernico, situa al Sol en el centro del movimiento de los planetas. Este ultimo modelo se ha demostrado que es el que se aplica en la realidad.

Leyes de Kepler

A comienzos del siglo XVIII Kepler anuncia sus tres leyes empiricas, es decir, basadas en la experimentacion, que rigen el movimiento de los planetas en torno al sol.

Ley de las orbitas

Los planetas giran alrededor del sol describiendo orbitas elipticas, en uno de cuyos focos se encuentra el sol.

perihelio afelio

Ley de las areas

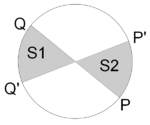
Las areas barridas por el radio vector que une el sol con un planeta son directamente proporcionales a los tiempos empleados en barrerlas.

El area barrida es directamente proporcional al tiempo

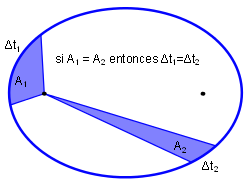
Si los tiempos empleados por el radio vector [math]\displaystyle{ \vec r }[/math] fueran iguales sucede que loas areas barridas son iguales, tal y como se indica en la imagen:

Esto implica que la velocidad orbital en 1 es mayor que la velocidad orbital en 2, es decir, es mayor en el perihelio:

Ley de los periodos

Los cuadrados de los periodos son directamente proporcionales a los cubos de los de los semiejes mayores de las respectivas orbitas

DIBUJO

[math]\displaystyle{ \frac {T_1^2}{r_1^3}=\frac{T_2^2}{r_1^3} }[/math]

Deducción de la Ley de la Gravitación Universal

En el siglo XVII Newton, basandose en las leyes de Kepler, dedujo la ley de la gravitacion universal basandose en las siguentes hipotesis.

• El sol y los planetas son particulas, ya uqe sus distancias relattivas son mayores que sus tamaños.
• El sistema de referencia es el sol, y la aceleracion de cada plaenta se mide con respecto del sol.
• Cada planeta describe una orbita circular con una aceleracion centripeta. [math]\displaystyle{ A_c = \frac {v^2}{r} }[/math]
• La unica fuerza significativa que actua sobre un planeta es la fuerza gravitatoria del sol, es decir, que la orbita de un planeta no se ve afectada por el movimiento del resto de planetas.

Si suponemos que los planetas describen una orbita circular, segun la segunda ley de Kepler, se cumple que:

[math]\displaystyle{ \Delta t_1 = \Delta t_2 \Leftrightarrow A_1 = A_2 }[/math] [math]\displaystyle{ S_1 = S_2 \Rightarrow v = \frac {S}{t} }[/math]

Siendo S la distancia recorrida por el planeta en el espacio.

De esto deducimos que [math]\displaystyle{ v_1 \Delta t_1 = v_2 \Delta t_2 }[/math] dado que [math]\displaystyle{ \Delta t_1 = \Delta t_2 }[/math], por lo que [math]\displaystyle{ v_1 = v_2 }[/math] en MCU, por lo que es constante.