Diferencia entre revisiones de «Memoria de practicas: Corriente continua»
m (Inigosendino movió la página Memorias corriente continua a Memoria de practicas: Corriente continua) |
|||
| (No se muestran 19 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
== | == Introducción y objetivos == | ||
En estas tres practicas se tienen como objetivo observar de forma practica el efecto que produce la | En estas tres practicas se tienen como objetivo observar de forma practica el efecto que produce la colocación de diferentes elementos en diferentes distribuciones con respecto a la tensión y a la corriente eléctrica. En este caso, tenemos tres circuitos formados por una fuente de corriente continua y varias resistencias. Los valores de ambas son diferentes en cada practica. | ||
== Lista de materiales == | == Lista de materiales == | ||
* Fuente de | * Fuente de alimentación Promax FAC363B | ||
* Polimetro Promax PD693 | * Polimetro Promax PD693 | ||
* Tablero de laboratorio | * Tablero de laboratorio | ||
| Línea 13: | Línea 13: | ||
[[Archivo:Practica 1 cc.png|400px]] | [[Archivo:Practica 1 cc.png|400px]] | ||
=== | === Cálculos previos === | ||
Al ser resistencias en serie se suman sus valores | Al ser resistencias en serie se suman sus valores | ||
| Línea 23: | Línea 23: | ||
<math>V=IR \Leftrightarrow I= \frac {V}{R} \Rightarrow I= \frac {10}{947}=0.01055A=10.55mA</math> | <math>V=IR \Leftrightarrow I= \frac {V}{R} \Rightarrow I= \frac {10}{947}=0.01055A=10.55mA</math> | ||
La tensión que tenga cada resistencia se calcula con la intensidad total y el valor de la resistencia, siendo la suma de los resultados la | La tensión que tenga cada resistencia se calcula con la intensidad total y el valor de la resistencia, siendo la suma de los resultados la tensión que proporciona la fuente. | ||
<math>V_1=IR_1 \Rightarrow V_1=0.01055 \cdot 220=2.323V</math><br> | <math>V_1=IR_1 \Rightarrow V_1=0.01055 \cdot 220=2.323V</math><br> | ||
| Línea 29: | Línea 29: | ||
<math>V_3=IR_3 \Rightarrow V_3=0.01055 \cdot 680=7.174V</math><br> | <math>V_3=IR_3 \Rightarrow V_3=0.01055 \cdot 680=7.174V</math><br> | ||
=== | ===Ejecución=== | ||
En este caso no surgieron complicaciones a la hora de ejecutar esta tarea. De hecho, los valores medidos y los calculados son mas | En este caso no surgieron complicaciones a la hora de ejecutar esta tarea. De hecho, los valores medidos y los calculados son mas próximos entre si en este ejercicio que en los demás. Los valores medidos fueron estos: | ||
<math>R_T=938\Omega ; I= 10,6mA ; V_1=2,31V; V_2=0,5V; V_3=7,2V</math> | <math>R_T=938\Omega ; I= 10,6mA ; V_1=2,31V; V_2=0,5V; V_3=7,2V</math> | ||
| Línea 48: | Línea 48: | ||
== Practica 2 == | == Practica 2 == | ||
=== | |||
[[Archivo:Practica 2 cc.png|400px]] | |||
=== Cálculos previos === | |||
La resistencia equivalente es el inverso de la suma de los inversos. | La resistencia equivalente es el inverso de la suma de los inversos. | ||
R_T= | <math>R_T=\frac {1}{\frac {1}{R_1}+\frac {1}{R_2}+\frac {1}{R_3}} \Rightarrow R_T=\frac {1}{\frac {1}{1000}+\frac {1}{680}+\frac {1}{100}}=80.18\Omega</math> | ||
La tensión que existe es la misma en las tres resistencias. La intensidad, sin embargo, se divide. | |||
<math>V=IR \Leftrightarrow I= \frac {V}{R} \Rightarrow I_T= \frac {60}{80.18}=0.07483A=74.83mA</math><br> | |||
<math>I_1=\frac {V}{R_1} \Rightarrow I_1 = \frac {6}{1000}=6\cdot10^{-3}A=6mA</math><br> | |||
<math>I_2=\frac {V}{R_2} \Rightarrow I_2 = \frac {6}{680}=8,83\cdot10^{-3}A=8,83mA</math><br> | |||
<math>I_3=\frac {V}{R_3} \Rightarrow I_3 = \frac {6}{100}=0,06A=60mA</math> | |||
===Ejecución=== | |||
En esta practica el margen de error es superior a la anterior. Aun así, sigue siendo valido dado que el incremento en la resistencia total justifica menores valores de intensidad. Los valores medidos fueron estos: | |||
<math>R_T=82.9\Omega; I_T = 68.6mA; I_1= 4 mA; I_2=8,6mA; I_3= 55mA</math> | |||
Se observa claramente que la suma de las intensidades parciales da como resultado la intensidad total medida en un principio. | |||
===Cuestiones=== | |||
La | '''¿Que sucede en el circuito si la rama de R3 se deja en circuito abierto?''' | ||
La resistencia total variará ligeramente, y provocará un cambio en la intensidad total. Las intensidades parciales de las otras ramas no variarán, al no depender de la resistencia ni de la intensidad de la tercera. | |||
== Practica 3 == | |||
[[Archivo:Practica 3 cc.png|400px]] | |||
=== Cálculos previos === | |||
En este caso, la resistencia total es la suma de la primera y el calculo de la equivalente entre la segunda y la tercera. | |||
<math>R_{23}=\frac {1}{\frac {1}{R_2}+\frac {1}{R_3}} \Rightarrow R_{23}=\frac {1}{\frac {1}{1000}+\frac {1}{220}}=180,32\Omega</math><br><br> | |||
<math>R_T=R_1+R_{23}=47+180,32=227,32\Omega</math> | |||
La intensidad total se comparte entre la resistencia en serie, y se reparte en paralelo, al contrario que la tensión. | |||
<math>V=IR \Leftrightarrow I= \frac {V}{R} \Rightarrow I_T= \frac {8}{227,32}=0.03519A=35.19mA</math><br><br> | |||
<math>I_1=35.19mA; I_2=35.19mA</math><br> | |||
<math>V_1=I_1 \cdot R_1 \Rightarrow V_1=0.03519 \cdot 47=1.654V</math><br> | |||
<math>V_{23}=I_{23} \cdot R_{23} \Rightarrow V_{23}=0.03519 \cdot 180,32=6.346V</math><br><br> | |||
<math>I_2=\frac {V_{23}}{R_2} \Rightarrow I_2 = \frac {6.346}{220}=0.02884A</math><br><br> | |||
<math>I_3=\frac {V_{23}}{R_3} \Rightarrow I_3 = \frac {6.346}{1000}=0,00634A</math> | |||
===Ejecucion=== | |||
Los resultados de esta practica contienen también un margen de error dado que el valor real de las resistencias es superior al valor teórico de las mismas. Estos son los resultados: | |||
<math>R_T=233\Omega; I_T=34,4mA; I_1= 34,4mA; I_2= 28,9mA; I_3=6,3mA; V_1= 1,651V; V_{23}= 6,26V</math> | |||
Observamos claramente que las bases teóricas de reparto de intensidad y tensión se cumplen en la practica. De hecho, Vamos que la intensidad de las resistencias 2 y 3 suman el valor de la intensidad total, que también es el valor de la intensidad de la primera resistencia. Por otra parte, las resistencias 2 y 3 comparten tensión, y ambas con la resistencia 1 suman el total de la tensión de la fuente. | |||
Esta practica ha sido la mas compleja en su ejecución, dado que en varias ocasiones el polimetro devolvía resultados nulos o incorrectos. Esto se debía en la mayoría de ocasiones a la mala situación del polimetro con respecto a los demás elementos. De hecho, durante este ejercicio hubo que realizar un cambio de fusible al aparato, dado que una incorrecta medición había sobrepasado el limite de dicho fusible. | |||
===Cuestiones=== | |||
'''¿Como le afectara al comportamiento del circuito si eliminamos primero R1 y después R2?''' | |||
Al eliminar la resistencia 1 la resistencia total disminuirá, haciendo que la intensidad total aumente. Asimismo, el voltaje que comparten las resistencias restantes aumentará. Al retirar la resistencia 2 la resistencia total aumentará, produciendo el efecto contrario en la intensidad. El voltaje ahora será integro en esta resistencia. | |||
Revisión actual del 20:56 1 oct 2013
Introducción y objetivos
En estas tres practicas se tienen como objetivo observar de forma practica el efecto que produce la colocación de diferentes elementos en diferentes distribuciones con respecto a la tensión y a la corriente eléctrica. En este caso, tenemos tres circuitos formados por una fuente de corriente continua y varias resistencias. Los valores de ambas son diferentes en cada practica.
Lista de materiales
- Fuente de alimentación Promax FAC363B
- Polimetro Promax PD693
- Tablero de laboratorio
- Resistencias de 47Ω, 100Ω, 220Ω, 680Ω y 1kΩ.
- Cableado
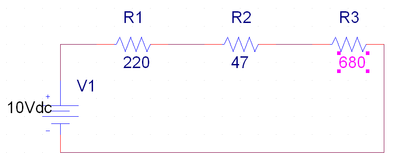
Practica 1
Cálculos previos
Al ser resistencias en serie se suman sus valores
[math]\displaystyle{ R_T=R_1+R_2+R_3=220+47+680=947\Omega }[/math]
La intensidad total se calcula con la ley de Ohm, y es igual para todas las resistencias.
[math]\displaystyle{ V=IR \Leftrightarrow I= \frac {V}{R} \Rightarrow I= \frac {10}{947}=0.01055A=10.55mA }[/math]
La tensión que tenga cada resistencia se calcula con la intensidad total y el valor de la resistencia, siendo la suma de los resultados la tensión que proporciona la fuente.
[math]\displaystyle{ V_1=IR_1 \Rightarrow V_1=0.01055 \cdot 220=2.323V }[/math]
[math]\displaystyle{ V_2=IR_2 \Rightarrow V_2=0.01055 \cdot 47=0.496V }[/math]
[math]\displaystyle{ V_3=IR_3 \Rightarrow V_3=0.01055 \cdot 680=7.174V }[/math]
Ejecución
En este caso no surgieron complicaciones a la hora de ejecutar esta tarea. De hecho, los valores medidos y los calculados son mas próximos entre si en este ejercicio que en los demás. Los valores medidos fueron estos:
[math]\displaystyle{ R_T=938\Omega ; I= 10,6mA ; V_1=2,31V; V_2=0,5V; V_3=7,2V }[/math]
Asimismo, medimos la intensidad de cada resistencia individualmente, con el fin de comprobar si de hecho en los tres casos su valor es el mismo.
Cuestiones
¿Le afecta la presencia del amperimetro al valor de la intensidad?
No, el amperimetro actúa como un cable, con la peculiaridad de que mide la intensidad que pasa por el. No afecta en absoluto al funcionamiento del circuito. Sin embargo, a la hora de medir con este aparato hay que ser cauteloso para no provocar un cortocircuito parcial o total.
¿Que efecto tendría sobre el circuito quitar una de las resistencias?
La consecuencia de eliminar cualquiera de las resistencias seria el aumento de la intensidad, asi como del voltaje individual de cada una de ellas.
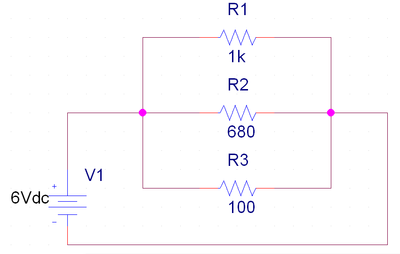
Practica 2
Cálculos previos
La resistencia equivalente es el inverso de la suma de los inversos.
[math]\displaystyle{ R_T=\frac {1}{\frac {1}{R_1}+\frac {1}{R_2}+\frac {1}{R_3}} \Rightarrow R_T=\frac {1}{\frac {1}{1000}+\frac {1}{680}+\frac {1}{100}}=80.18\Omega }[/math]
La tensión que existe es la misma en las tres resistencias. La intensidad, sin embargo, se divide.
[math]\displaystyle{ V=IR \Leftrightarrow I= \frac {V}{R} \Rightarrow I_T= \frac {60}{80.18}=0.07483A=74.83mA }[/math]
[math]\displaystyle{ I_1=\frac {V}{R_1} \Rightarrow I_1 = \frac {6}{1000}=6\cdot10^{-3}A=6mA }[/math]
[math]\displaystyle{ I_2=\frac {V}{R_2} \Rightarrow I_2 = \frac {6}{680}=8,83\cdot10^{-3}A=8,83mA }[/math]
[math]\displaystyle{ I_3=\frac {V}{R_3} \Rightarrow I_3 = \frac {6}{100}=0,06A=60mA }[/math]
Ejecución
En esta practica el margen de error es superior a la anterior. Aun así, sigue siendo valido dado que el incremento en la resistencia total justifica menores valores de intensidad. Los valores medidos fueron estos:
[math]\displaystyle{ R_T=82.9\Omega; I_T = 68.6mA; I_1= 4 mA; I_2=8,6mA; I_3= 55mA }[/math]
Se observa claramente que la suma de las intensidades parciales da como resultado la intensidad total medida en un principio.
Cuestiones
¿Que sucede en el circuito si la rama de R3 se deja en circuito abierto?
La resistencia total variará ligeramente, y provocará un cambio en la intensidad total. Las intensidades parciales de las otras ramas no variarán, al no depender de la resistencia ni de la intensidad de la tercera.
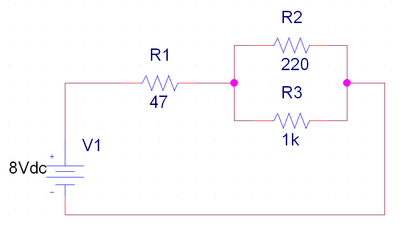
Practica 3
Cálculos previos
En este caso, la resistencia total es la suma de la primera y el calculo de la equivalente entre la segunda y la tercera.
[math]\displaystyle{ R_{23}=\frac {1}{\frac {1}{R_2}+\frac {1}{R_3}} \Rightarrow R_{23}=\frac {1}{\frac {1}{1000}+\frac {1}{220}}=180,32\Omega }[/math]
[math]\displaystyle{ R_T=R_1+R_{23}=47+180,32=227,32\Omega }[/math]
La intensidad total se comparte entre la resistencia en serie, y se reparte en paralelo, al contrario que la tensión.
[math]\displaystyle{ V=IR \Leftrightarrow I= \frac {V}{R} \Rightarrow I_T= \frac {8}{227,32}=0.03519A=35.19mA }[/math]
[math]\displaystyle{ I_1=35.19mA; I_2=35.19mA }[/math]
[math]\displaystyle{ V_1=I_1 \cdot R_1 \Rightarrow V_1=0.03519 \cdot 47=1.654V }[/math]
[math]\displaystyle{ V_{23}=I_{23} \cdot R_{23} \Rightarrow V_{23}=0.03519 \cdot 180,32=6.346V }[/math]
[math]\displaystyle{ I_2=\frac {V_{23}}{R_2} \Rightarrow I_2 = \frac {6.346}{220}=0.02884A }[/math]
[math]\displaystyle{ I_3=\frac {V_{23}}{R_3} \Rightarrow I_3 = \frac {6.346}{1000}=0,00634A }[/math]
Ejecucion
Los resultados de esta practica contienen también un margen de error dado que el valor real de las resistencias es superior al valor teórico de las mismas. Estos son los resultados:
[math]\displaystyle{ R_T=233\Omega; I_T=34,4mA; I_1= 34,4mA; I_2= 28,9mA; I_3=6,3mA; V_1= 1,651V; V_{23}= 6,26V }[/math]
Observamos claramente que las bases teóricas de reparto de intensidad y tensión se cumplen en la practica. De hecho, Vamos que la intensidad de las resistencias 2 y 3 suman el valor de la intensidad total, que también es el valor de la intensidad de la primera resistencia. Por otra parte, las resistencias 2 y 3 comparten tensión, y ambas con la resistencia 1 suman el total de la tensión de la fuente.
Esta practica ha sido la mas compleja en su ejecución, dado que en varias ocasiones el polimetro devolvía resultados nulos o incorrectos. Esto se debía en la mayoría de ocasiones a la mala situación del polimetro con respecto a los demás elementos. De hecho, durante este ejercicio hubo que realizar un cambio de fusible al aparato, dado que una incorrecta medición había sobrepasado el limite de dicho fusible.
Cuestiones
¿Como le afectara al comportamiento del circuito si eliminamos primero R1 y después R2?
Al eliminar la resistencia 1 la resistencia total disminuirá, haciendo que la intensidad total aumente. Asimismo, el voltaje que comparten las resistencias restantes aumentará. Al retirar la resistencia 2 la resistencia total aumentará, produciendo el efecto contrario en la intensidad. El voltaje ahora será integro en esta resistencia.