Diferencia entre revisiones de «1. Movimiento armónico simple.»

Revisión actual del 16:27 26 dic 2012

Temario de Fisica (2012-2013)

Movimiento periódico

Se dice que un movimiento es periódico cuando se repite a intervalos regulares de tiempo.

Periodo (T): Es el tiempo empleado en repetir el movimiento. (unidades: s)
Frecuencia (f): numero de vueltas completas que realiza el móvil en la unidad de tiempo. (unidades: s^-1 ,Hz)

[math]\displaystyle{ f =\frac {1}{T} }[/math]

Movimiento vibratorio

Es uno de los movimientos mas importantes que se dan en la naturaleza. Es un movimiento armónico simple. Se denominan asi porque se pueden expresar mediante funciones armónicas (seno y coseno).

Ej: Sea una masa m unida a un resorte de constante elástica k. Suponemos que μ=0.

Simplificamos la ley de Hooke: [math]\displaystyle{ (F = k \Delta y i) }[/math] [math]\displaystyle{ |F| = k \Delta y i }[/math](N)

Periodo (T); Equivale al tiempo que tarda en realizar una oscilación completa.
La distancia entre O (el origen) y A (la elongación máxima) es la amplitud de vibración. Dicho desplazamiento se realiza en T/4.
Elongación (x): nos indica la posición de la partícula en cada instante.

Si anotamos y representamos gráficamente x del cuerpo respecto al tiempo, obtenemos funcion sinusoidal, y , por tanto, se trata de una función armónica.

Si la frecuencia es baja, hablamos de un movimiento ondulatorio. Si la frecuencia es alta, es un movimiento vibratorio.

Ecuaciones del Movimiento armónico simple

El movimiento armónico simple de trayectoria recta se puede considerar como la proyección sobre un diámetro del Movimiento circular uniforme.

Vamos a desarrollar la ecuación de posición:

Sea una partícula describiendo un Movimiento circular uniforme.

[math]\displaystyle{ cos [\frac{\pi}{2} - (\varphi_0 + \omega t)] = \frac {x}{A} }[/math]

[math]\displaystyle{ x = A cos [\frac{\pi}{2} - (\varphi_0 + \omega t)] }[/math]

[math]\displaystyle{ x = A sin (\varphi_0 + \omega t) }[/math] (m)

Magnitudes principales del Movimiento armónico simple

Elongación: x(t) describe la posición de la partícula respecto al origen. (unidades: m)
Amplitud (A): Es el valor máximo que puede tomar la elongación. (unidades: m)
Frecuencia angular (ω): Representa la velocidad angular constante del Movimiento circular uniforme asociado. (unidades: rad/s)

[math]\displaystyle{ \omega = \frac {2\pi}{T} }[/math];[math]\displaystyle{ \omega = 2\pi f }[/math]

Fase inicial (φ₀): indica el estado de la vibracion de la particula en el instante inicial. (unidades: rad)
Fase en cualquier estado (ωt+φ₀): indica el estado de la vibración de la partícula en el cualquier instante. (unidades: rad)
Periodo (T): Es el tiempo empleado en repetir el movimiento. (unidades: s)
Frecuencia (f): numero de vibraciones completas que realiza la partícula en la unidad de tiempo. (unidades: s^-1 ,Hz)

Cinemática del Movimiento armónico simple

Velocidad del Movimiento armónico simple

[math]\displaystyle{ v= \frac {dx}{dt}=\frac {dx(t)}{dt}=\frac {d[A sin(\omega t+\varphi_0)]}{dt} }[/math]

[math]\displaystyle{ v (t)= A \omega cos(\omega t+\varphi_0) }[/math](m/s)

Desarrollamos la ecuación aplicando [math]\displaystyle{ cos^2\alpha + sin^2\alpha = 1 \Leftrightarrow cos\alpha= \pm \sqrt {1-sin^2\alpha} }[/math] :

[math]\displaystyle{ v (t)= \pm A \omega \sqrt {1-sin^2 (\omega t+\varphi_0)} \Leftrightarrow v (t)= \pm \omega \sqrt {A^2-A^2 sin^2 (\omega t+\varphi_0)} }[/math] Simplificando deducimos que: [math]\displaystyle{ v (t)= \pm \omega \sqrt {A^2-x^2} }[/math] (m/s)

También podemos concluir que:

La velocidad depende de la posicion y es periodica.
Los signos +/- indican el sentido del movimiento segun los ejes cartesianos.
La velocidad máxima siemore se dará en el centro de la trayectoria y su formula será [math]\displaystyle{ v_{max} = \pm A \omega }[/math]

Aceleración del Movimiento armónico simple

[math]\displaystyle{ a= \frac {dv}{dt}=\frac {d[A \omega cos(\omega t+\varphi_0)]}{dt} }[/math]

[math]\displaystyle{ v (t)= -A \omega^2 sin(\omega t+\varphi_0)=-\omega^2 x }[/math] (m/s²)

[math]\displaystyle{ \varphi_0, tg \varphi_0 }[/math] [math]\displaystyle{ x=A sin (\omega t + \varphi_0); v= A \omega cos(\omega t+\varphi_0) }[/math] [math]\displaystyle{ t_0 \rightarrow x_0=A sin \varphi_0; v= A \omega cos\varphi_0 }[/math] [math]\displaystyle{ \frac {x_0}{v_0}=\frac {A sin \varphi_0}{A \omega cos\varphi_0} = \frac {tg \varphi_0}{\omega} }[/math] [math]\displaystyle{ tg \varphi_0 = \frac {x_0 \omega}{v_0} \rightarrow \varphi_0 = arctg (\frac {x_0 \omega}{v_0}) }[/math]

Concluimos que:

La aceleración máxima siempre se dará en los extremos de la trayectoria y su formula será [math]\displaystyle{ v_{max} = \pm A \omega^2 }[/math]
La velocidad mínima siempre se dará en el centro de la trayectoria y su valor será 0.

Dinámica del Movimiento armónico simple

Resorte horizontal

Sea una masa m unida a un resorte de constante elástica recuperadora k

* 2ª ley Newton: [math]\displaystyle{ \sum F = m a \Rightarrow F_e=ma }[/math]

Aplicamos la ley de Hooke [math]\displaystyle{ F_e=-k \Delta x }[/math]

[math]\displaystyle{ -k \Delta x=m a_x=m (-\omega^2 x) \Leftrightarrow -kx=-m \omega^2x }[/math]

Simplificando hallamos que [math]\displaystyle{ k=m\omega^2 }[/math] (N/m)

De esta ecuación también podemos deducir lo siguiente:

[math]\displaystyle{ \omega = \sqrt {\frac {k}{m}}\Rightarrow 2\pi f= \sqrt {\frac {k}{m}}\Rightarrow f=\frac {1}{2\pi}\sqrt {\frac {k}{m}} }[/math]

Masa colgada de un resorte vertical

Sea un resorte vertical de constante recuperadora k del que cuelga una masa m

Al colgar la masa m se producirá un estiramiento, como consecuencia del peso [math]\displaystyle{ (\Delta l) }[/math]

2ª ley Newton: [math]\displaystyle{ \sum F =0 }[/math]

Eje y: [math]\displaystyle{ F_e = P }[/math]

Aplicamos [math]\displaystyle{ F_e=-k\Delta l \Leftrightarrow F_e = -k (-l-0)=+kl }[/math]

[math]\displaystyle{ kl=mg \Rightarrow k= \frac {mg}{l} }[/math] (N/m)

[math]\displaystyle{ f=\frac {1}{2\pi}\sqrt {\frac {k}{m}} }[/math]

Pendulo simple

Una masa m, colgada de un hilo de longitud l cuya masa es despreciable, se mueve sin rozamiento en un angulo [math]\displaystyle{ \theta }[/math]

Sigue un movimiento armónico simple en el eje OX, por lo que cumple sus normas. Ademas, podemos hallar el valor de F_x o F_t

[math]\displaystyle{ F_t=-mg sin \theta }[/math]

En pequeños ángulos podemos decir que [math]\displaystyle{ \theta = sin \theta }[/math]

[math]\displaystyle{ F_t=-mg \theta= -mg \frac {x}{l} }[/math]

Aplicando [math]\displaystyle{ k= \frac {mg}{l} }[/math] deducimos que:

[math]\displaystyle{ F_t=-kx }[/math]

La aceleración sera:

[math]\displaystyle{ a= \frac {F_t}{m} = -\frac {k}{m}x }[/math]

El periodo de este movimiento es:

[math]\displaystyle{ T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{l}{g}} }[/math]

El periodo no depende ni de la amplitud ni de la frecuencia angular.

@@ Línea 1: / Línea 1: @@
 Temario de [[Fisica]] (2012-2013)
-==Movimiento periodico==
+==Movimiento periódico ==
-Se dice que un movimiento es periodico cuando se repite a intervalos regulares de tiempo.
+Se dice que un movimiento es periódico cuando se repite a intervalos regulares de tiempo.
 * Periodo (T): Es el tiempo empleado en repetir el movimiento. (unidades: s)
-* Frecuencia (f): nuemro de vueltas completas qe realiza el movil en la unidad de tiempo. (unidades: s<sup>-1</sup> ,Hz)
+* Frecuencia (f): numero de vueltas completas que realiza el móvil en la unidad de tiempo. (unidades: s<sup>-1</sup> ,Hz)
 <center><math>f =\frac {1}{T}</math></center>
@@ Línea 12: / Línea 12: @@
 ==Movimiento vibratorio==
-Es uno de los movimientos mas importantes que se dan en la naturaleza. Es un movimiento armonico simple. Se denominan asi porque se pueden expresar mediante funciones armonicas (seno y coseno).
+Es uno de los movimientos mas importantes que se dan en la naturaleza. Es un movimiento armónico simple. Se denominan asi porque se pueden expresar mediante funciones armónicas (seno y coseno).
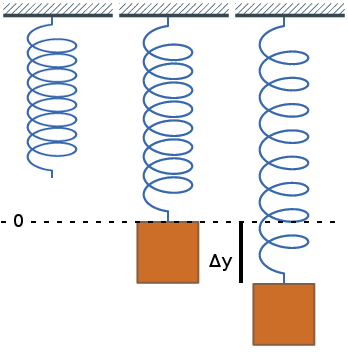
-Ej: Sea una masa m unida a un resorte de constante elastica k. Suponemos que μ=0.
+Ej: Sea una masa m unida a un resorte de constante elástica k. Suponemos que μ=0.
 [[File:Resortes.png|center]]
@@ Línea 22: / Línea 22: @@
 <center><math>|F| = k \Delta y i</math>(N)</center>
-* Periodo (T); Equivale al tiempo que tarda en realizar una oscilacion completa.
+* Periodo (T); Equivale al tiempo que tarda en realizar una oscilación completa.
-* La distancia entre O (el origen) y A (la elongacion maxima) es la amplitud de vibracion. Dicho desplazamiento se realiza en T/4.
+* La distancia entre O (el origen) y A (la elongación máxima) es la amplitud de vibración. Dicho desplazamiento se realiza en T/4.
-* Elongacion (x): nos indica la posicion de la particula en cada instante.
+* Elongación (x): nos indica la posición de la partícula en cada instante.
-Si anotamos y representamos graficamente x del cuerpo respecto al tiempo, obtenemos funcion sinusoidal, y , por tanto, se trata de una funcion armonica.
+Si anotamos y representamos gráficamente x del cuerpo respecto al tiempo, obtenemos funcion sinusoidal, y , por tanto, se trata de una función armónica.
 [[File:Onda.png|400px|center]]
@@ Línea 34: / Línea 34: @@
 == Ecuaciones del Movimiento armónico simple==
-El movimiento armónico simple de trayectoria recta se puede considerar como la proyeccion sobre un diametro del Movimiento circular uniforme.
+El movimiento armónico simple de trayectoria recta se puede considerar como la proyección sobre un diámetro del Movimiento circular uniforme.
-Vamos a desarrollar la ecuacion de posicion:
+Vamos a desarrollar la ecuación de posición:
+<center>Sea una partícula describiendo un Movimiento circular uniforme.</center>
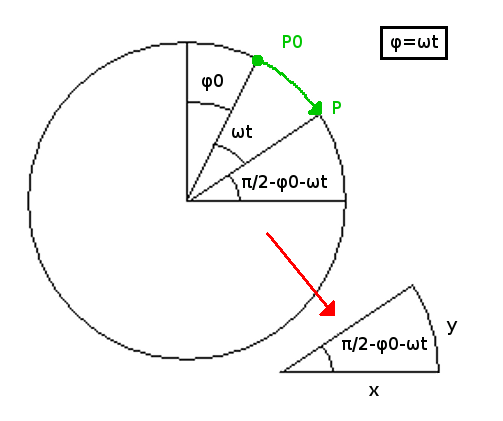
-<center>Sea una particula describiendo un Movimiento circular uniforme.</center>
+<center>[[File:Mcu.PNG]]</center>
+<center><math>cos [\frac{\pi}{2} - (\varphi_0 + \omega t)] = \frac {x}{A}</math></center>
+<center><math>x = A cos [\frac{\pi}{2} - (\varphi_0 + \omega t)]</math></center>
-<center>cos ( π/2 - (φ<sub>0</sub> + ωt) = x/A</center>
-<center>x = A cos [ π/2 - (φ<sub>0</sub> + ωt)]</center>
+<center><math>x = A sin (\varphi_0 + \omega t)</math> (m)</center>
-<center>'''x = A sen (ωt + φ<sub>0</sub>)''' (m)</center>
 ==Magnitudes principales del Movimiento armónico simple==
-* Elongacion: x(t) describe la posiciom de la particula respecto al origen. (unidades: m)
+* Elongación: x(t) describe la posición de la partícula respecto al origen. (unidades: m)
-* Amplitud (A): Es el valor maximo que puede tomar la elongacion. (unidades: m)
+* Amplitud (A): Es el valor máximo que puede tomar la elongación. (unidades: m)
 * Frecuencia angular (ω): Representa la velocidad angular constante del Movimiento circular uniforme asociado. (unidades: rad/s)
-<center>ω = 2π/T ω = 2πf</center>
+<center><math>\omega = \frac {2\pi}{T}</math>;<math>\omega = 2\pi f</math></center>
 * Fase inicial (φ<sub>0</sub>): indica el estado de la vibracion de la particula en el instante inicial. (unidades: rad)
-* Fase en cualquier estado (ωt+φ<sub>0</sub>): indica el estado de la vibracion de la particula en el cualquier instante. (unidades: rad)
+* Fase en cualquier estado (ωt+φ<sub>0</sub>): indica el estado de la vibración de la partícula en el cualquier instante. (unidades: rad)
 * Periodo (T): Es el tiempo empleado en repetir el movimiento. (unidades: s)
-* Frecuencia (f): numero de vibraciones completas que realiza la particula en la unidad de tiempo. (unidades: s<sup>-1</sup> ,Hz)
+* Frecuencia (f): numero de vibraciones completas que realiza la partícula en la unidad de tiempo. (unidades: s<sup>-1</sup> ,Hz)
+== Cinemática del Movimiento armónico simple==
+===Velocidad del Movimiento armónico simple===
+<center><math>v= \frac {dx}{dt}=\frac {dx(t)}{dt}=\frac {d[A sin(\omega t+\varphi_0)]}{dt}</math></center>
+<center><math>v (t)= A \omega cos(\omega t+\varphi_0)</math>(m/s)</center>
+Desarrollamos la ecuación aplicando <math>cos^2\alpha + sin^2\alpha = 1 \Leftrightarrow cos\alpha= \pm \sqrt {1-sin^2\alpha}</math> :
+<center><math>v (t)= \pm A \omega \sqrt {1-sin^2 (\omega t+\varphi_0)} \Leftrightarrow v (t)= \pm \omega \sqrt {A^2-A^2 sin^2 (\omega t+\varphi_0)}</math></center>
+<center> Simplificando deducimos que: <math>v (t)= \pm \omega \sqrt {A^2-x^2}</math> (m/s)</center>
+También podemos concluir que:
+* La velocidad depende de la posicion y es periodica.
+* Los signos +/- indican el sentido del movimiento segun los ejes cartesianos.
+* La velocidad máxima siemore se dará en el centro de la trayectoria y su formula será <math>v_{max} = \pm A \omega</math>
+=== Aceleración del Movimiento armónico simple===
+<center><math>a= \frac {dv}{dt}=\frac {d[A \omega cos(\omega t+\varphi_0)]}{dt}</math></center>
+<center><math>v (t)= -A \omega^2 sin(\omega t+\varphi_0)=-\omega^2 x</math> (m/s<sup>2</sup>)</center>
+{| class="wikitable"
+|<math>\varphi_0, tg \varphi_0</math>
+<math>x=A sin (\omega t + \varphi_0); v= A \omega cos(\omega t+\varphi_0)</math>
+<math>t_0 \rightarrow x_0=A sin \varphi_0; v= A \omega cos\varphi_0</math>
+<math>\frac {x_0}{v_0}=\frac {A sin \varphi_0}{A \omega cos\varphi_0} = \frac {tg \varphi_0}{\omega}</math>
+<math>tg \varphi_0 = \frac {x_0 \omega}{v_0} \rightarrow \varphi_0 = arctg (\frac {x_0 \omega}{v_0})</math>
+|-
+|}
+Concluimos que:
+* La aceleración máxima siempre se dará en los extremos de la trayectoria y su formula será <math>v_{max} = \pm A \omega^2</math>
+* La velocidad mínima siempre se dará en el centro de la trayectoria y su valor será 0.
+== Dinámica del Movimiento armónico simple==
+===Resorte horizontal===
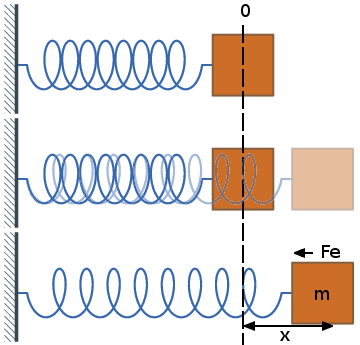
+Sea una masa m unida a un resorte de constante elástica recuperadora k
+[[File:1.6.1.png|center]]
+<nowiki>*</nowiki> 2ª ley Newton: <math>\sum F = m a \Rightarrow F_e=ma</math>
+Aplicamos la ley de Hooke <math>F_e=-k \Delta x</math>
+<math>-k \Delta x=m a_x=m (-\omega^2 x) \Leftrightarrow -kx=-m \omega^2x </math>
+Simplificando hallamos que <math>k=m\omega^2</math> (N/m)
+De esta ecuación también podemos deducir lo siguiente:
+<math>\omega = \sqrt {\frac {k}{m}}\Rightarrow 2\pi f= \sqrt {\frac {k}{m}}\Rightarrow f=\frac {1}{2\pi}\sqrt {\frac {k}{m}} </math>
+===Masa colgada de un resorte vertical===
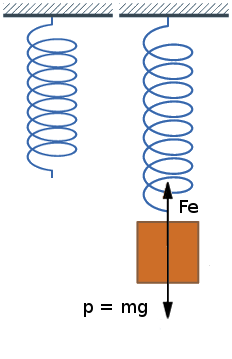
+Sea un resorte vertical de constante recuperadora k del que cuelga una masa m
+[[File:1.6.2.png|center]]
+Al colgar la masa m se producirá un estiramiento, como consecuencia del peso <math>(\Delta l)</math>
+ª ley Newton: <math>\sum F =0</math>
+Eje y: <math>F_e = P</math>
+Aplicamos <math>F_e=-k\Delta l \Leftrightarrow F_e = -k (-l-0)=+kl</math>
+<math>kl=mg \Rightarrow k= \frac {mg}{l}</math> (N/m)
+{| class="wikitable"
+|<math>f=\frac {1}{2\pi}\sqrt {\frac {k}{m}}</math>
+|-
+|}
+===Pendulo simple===
+[[File:PenduloSimple.jpg]]
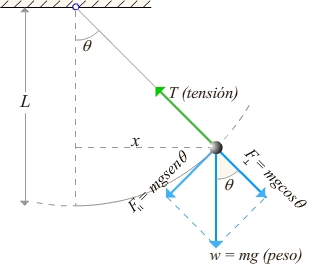
+Una masa m, colgada de un hilo de longitud l cuya masa es despreciable, se mueve sin rozamiento en un angulo <math>\theta</math>
+Sigue un movimiento armónico simple en el eje OX, por lo que cumple sus normas. Ademas, podemos hallar el valor de F<sub>x</sub> o F<sub>t</sub>
+<math>F_t=-mg sin \theta</math>
+En pequeños ángulos podemos decir que <math>\theta = sin \theta</math>
-==Cinematica del Movimiento armónico simple==
+<math>F_t=-mg \theta= -mg \frac {x}{l}</math>
+Aplicando <math>k= \frac {mg}{l}</math> deducimos que:
+<math>F_t=-kx</math>
+La aceleración sera:
+<math>a= \frac {F_t}{m} = -\frac {k}{m}x</math>
+El periodo de este movimiento es:
-ω
+<math>T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{l}{g}}</math>
+El periodo no depende ni de la amplitud ni de la frecuencia angular.
-φ
+== Energía==

Anónimo

Buscar

Diferencia entre revisiones de «1. Movimiento armónico simple.»

Espacios de nombres

Más

Acciones de página

Revisión actual del 16:27 26 dic 2012

Sumario

Movimiento periódico

Movimiento vibratorio

Ecuaciones del Movimiento armónico simple

Magnitudes principales del Movimiento armónico simple