Diferencia entre revisiones de «7. Campo magnético»
De Portfolio Academico
| Línea 18: | Línea 18: | ||
Utilizando la Ley de Lorentz, podemos determinar la fuerza magnetica que aparece sobre la particula. | Utilizando la Ley de Lorentz, podemos determinar la fuerza magnetica que aparece sobre la particula. | ||
<center><math>\vec F = q (\vec v \times \vec B)</math></center | <center><math>\vec F = q (\vec v \times \vec B)</math></center> | ||
Resolvemos vectorialmente este producto por la regla de sarrus. | Resolvemos vectorialmente este producto por la regla de sarrus. | ||
[[Archivo:Sarrus3.jpg]] | |||
<math>F= \hat i v_y B_z + \hat j v_z B_x + \hat k v_x B_y - ( \hat k v_y B_x + \hat j v_x B_z + \hat i v_z B_y)</math> | |||
Revisión del 18:14 30 ene 2013
Pertenece al temario de Fisica
Campo magnetico
- Campo [math]\displaystyle{ \vec B }[/math]
- Induccion
- Unidades
- Lineas -> Cerradas
- Flujo
- Iman: Un iman es un dipolo magnetico que crea a su alrededor un campo magnetico y, por tanto, altera las propiedades del espacio.
Ley de Lorentz
Colocamos una particula de carga q entre dos imanes, con una velocidad v. Entre los dos imanes se creará un campo magnetico.
DIBUJO
Utilizando la Ley de Lorentz, podemos determinar la fuerza magnetica que aparece sobre la particula.
Resolvemos vectorialmente este producto por la regla de sarrus.
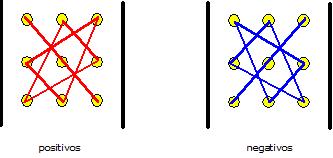[math]\displaystyle{ F= \hat i v_y B_z + \hat j v_z B_x + \hat k v_x B_y - ( \hat k v_y B_x + \hat j v_x B_z + \hat i v_z B_y) }[/math]
